---

 

Система счисления и логика

Ключевые слова:

• система счисления
• цифра
• алфавит
• позиционная система счисления
• основание
• высказывание

Система счисления

Система счисления — это знаковая система, в которой приняты определённые правила записи чисел. Знаки, с помощью которых записываются числа (рис. 1.1), называются цифрами, а их совокупность — алфавитом системы счисления. (Правило)

В любой системе счисления цифры служат для обозначения чисел, называемых узловыми; остальные числа (алгоритмические) получаются в результате каких либо операций из узловых чисел.

Пример 1. У вавилонян узловыми являлись числа 1, 10, 60; в римской системе счисления узловые числа — это 1, 5, 10, 50, 100, 500 и 1000, обозначаемые соответственно I, V, X, L, С, D, М.

Рис. 1.1. Знаки, используемые для записи чисел в различных системах счисления

История развития систем счисления

Системы счисления различаются выбором узловых чисел и способами образования алгоритмических чисел. Можно выделить следующие виды систем счисления:

• унарная система;
• непозиционные системы;
• позиционные системы.

Простейшая и самая древняя система — так называемая унарная система счисления. В ней для записи любых чисел используется всего один символ — палочка, узелок, зарубка, камушек.

Система счисления называется непозиционной, если количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа.

Пример 2. В древнеегипетской системе счисления числа обозначались соответственно следующим образом: 1, 2, 3, 4, 10, 13, 40.

Те же числа в римской системе счисления обозначаются так: I, II, III, IV, X, XIII, XL. Здесь алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.

Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (позиции) в записи числа. Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.

Десятичная система записи чисел — пример позиционной системы счисления. Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Основанием позиционной системы счисления может служить любое натуральное число q > 1. Алфавитом произвольной позиционной системы счисления с основанием q служат числа 0, 1, ..., q—1, каждое из которых может быть записано с помощью одного уникального символа; младшей цифрой всегда является 0.

Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов, необходимых для записи любых чисел.

Развернутая форма записи числа

В позиционной системе счисления с основанием q любое число может быть представлено в виде: A_q = ± (а_n-1 • q^n-1 + а_n-2 • q^n-2 + ... + a_о • q  + a_-1 • q^-1 + ... + а_-m • q^-m).

Здесь:

А— число;

q— основание системы счисления;

a_i— цифры, принадлежащие алфавиту данной системы счисления;

п— количество целых разрядов числа;

т— количество дробных разрядов числа;

qⁱ— «вес» i-гo разряда.

Пример 3. Рассмотрим десятичное число 14351,1. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме переходим к развёрнутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:

1 • 10⁴ + 4 • 10³ + 3 • 10² + 5 • 10¹ + 1 • 10  + 1 • 10^-1.

Представим таблицу соответствия десятичных, двоичных, восьмеричных и шестнадцатеричных чисел от 0 до 20₁₀

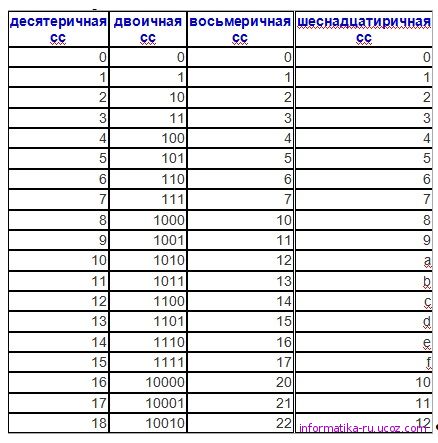
Двоичная система счисления

Двоичной системой счисления называется позиционная система счисления с основанием 2.

Для записи чисел в двоичной системе счисления используются только две цифры: 0 и 1.

На основании формулы (1) для целых двоичных чисел можно записать:

а_n-1 а_n-2...а₁а₀ = а_n-1 • 2^n-1 + а_n-2 •2^n-2+…+a₀•2⁰

Например:

10011₂ = 1 • 2⁴ + 0 • 2³ + 0 • 2² + 1•2¹ + 1 • 2⁰ = 2⁴ + 2¹ + 2⁰ = 19₁₀

Такая форма записи «подсказывает» правило перевода натуральных двоичных чисел в десятичную систему счисления: необходимо вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.

Получим правило перевода целых десятичных чисел в двоичную систему счисления из формулы (1).

Разделим аn-1 • 2^n-1 + а_n-2 •2^n-2+…+a₀•2⁰ на 2. Частное будет равно а_n-1 •2^n-2 + ... + а₁, а остаток будет равен а₀.

Полученное частное опять разделим на 2, остаток от деления будет равен а1.

Если продолжить этот процесс деления, то на n-м шаге получим набор цифр:

а₀, а₁, а₂, ..., а_n-1 ,

которые входят в двоичное представление исходного числа и совпадают с остатками при его последовательном делении на 2.

Таким образом, для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на 2 до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример 4. Переведём десятичное число 11 в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:

Выписывая остатки от деления в направлении, указанном стрелкой, получим: 1110 = 10112.

Пример 5. Если десятичное число достаточно большое, то более удобен следующий способ записи рассмотренного выше алгоритма:

Пример кодирования

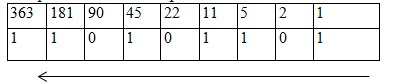
363₁₀ = 101101011₂

Правило перевода целых десятичных чисел в систему счисления с основанием q

Для перевода целого десятичного числа в систему счисления с основанием q следует:

1. последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, равное нулю;
2. полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
3. составить число в новой системе счисления, записывая его, на­чиная с последнего полученного остатка.

Представим таблицу соответствия десятичных, двоичных, восьмеричных и шестнадцатеричных чисел от О до 20₁₀.

Правило перевода недесятичных чисел в десятичную систему счисления 

Преобразование десятичного числа

Интерактивный задачник по  системам счисления

Правило перевода

Основы логики

Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами. Многие математические объекты (целые и рациональные числа, многочлены, векторы, множества) вы изучаете в школьном курсе алгебры, где знакомитесь с такими разделами математики, как алгебра чисел, алгебра многочленов, алгебра множеств и т. д.

Для информатики важен раздел математики, называемый алгеброй логики; объектами алгебры логики являются высказывания.

Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.

Например, относительно предложений «Великий русский учёный М. В. Ломоносов родился в 1711 году» и «Two plus six is eight» можно однозначно сказать, что они истинны. Предложение «Зимой воробьи впадают в спячку» ложно. Следовательно, эти предложения являются высказываниями.

Например, предложение «Это предложение является ложным» не является высказыванием, так как относительно него нельзя сказать, истинно оно или ложно, без того чтобы не получить противоречие. Действительно, если принять, что предложение истинно, то это противоречит сказанному. Если же принять, что предложение ложно, то отсюда следует, что оно истинно.

Побудительные и вопросительные предложения высказываниями не являются

Высказывания могут строиться с использованием знаков различных формальных языков — математики, физики, химии и т. п.

Не являются высказываниями числовые выражения, но из двух числовых выражений можно составить высказывание, соединив их знаками равенства или неравенства. Например:

1)«3 + 5 = 2 • 4» (истинное высказывание);

2)«II + VI > VIII» (ложное высказывание).

Не являются высказываниями и равенства или неравенства, содержащие переменные. Например, предложение «X < 12» становится высказыванием только при замене переменной каким-либо конкретным значением: «5 < 12» — истинное высказывание; «12 < 12» — ложное высказывание.

Обоснование истинности или ложности высказываний решается теми науками, к сфере которых они относятся. Алгебра логики отвлекается от смысловой содержательности высказываний. Её интересует только то, истинно или ложно данное высказывание. В алгебре логики высказывания обозначают буквами и называют логическими переменными. При этом если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей (А = 1), а если ложно — нулём {В = 0). 0 и 1, обозначающие значения логических переменных, называются логическими значениями.

Алгебра логики определяет правила записи, упрощения и преобразования высказываний и вычисления их значений.

Оперируя логическими переменными, которые могут быть равны только 0 или 1, алгебра логики позволяет свести обработку информации к операциям с двоичными данными. Именно аппарат алгебры логики положен в основу компьютерных устройств хранения и обработки данных. С применением элементов алгебры логики вы будете встречаться и во многих других разделах информатики.

Построение таблиц истинности

Для логического выражения можно построить таблицу истинности, показывающую, какие значения принимает выражение при всех наборах значений входящих в него переменных. Для построения таблицы истинности следует:

1. подсчитать п — число переменных в выражении;
2. подсчитать общее число логических операций в выражении;
3. установить последовательность выполнения логических операций с учётом скобок и приоритетов;
4. определить число столбцов в таблице: число переменных + число операций;
5. заполнить шапку таблицы, включив в неё переменные и операции в соответствии с последовательностью,  установленной в п. 3;
6. определить число строк в таблице (не считая шапки таблицы):

      m = 2ⁿ;

7. выписать наборы входных переменных с учётом того, что они представляют собой ряд целых n-разрядных двоичных чисел от 0 до 2 ⁿ -1;
8. провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью.

Построим таблицу истинности для логического выражения A v A & В. В нём две переменные, две операции, причём сначала выполняется конъюнкция, а затем — дизъюнкция. Всего в таблице будет четыре столбца:

А&В

As/A&B

Наборы входных переменных — это целые числа от 0 до 3, пред­ставленные в двухразрядном двоичном коде: 00, 01, 10, 11. Заполненная таблица истинности имеет вид:

Обратите внимание, что последний столбец (результат) совпал со столбцом А. В таком случае говорят, что логическое выражение A v A& В равносильно логической переменной А.

Свойства логических операций

Рассмотрим основные свойства логических операций, называемые также законами алгебры логики.

1. Переместительный (коммутативный) закон:

• для логического умножения:  А&В = В&А;

• для логического сложения:  AvB = BvA.

2. Сочетательный (ассоциативный) закон:

• для логического умножения:

• для логического сложения: (AvB)vC = Av (BvC).

При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.

3. Распределительный (дистрибутивный) закон:

• для логического умножения: A&(BvC) = (A&B)v(A& С);

•для логического сложения:  A v (В & С) = (A v В) & (A v С).

4. Закон двойного отрицания: А=А. Двойное отрицание исключает отрицание.

5. Закон исключённого третьего:

•для логического умножения: А & А = О;

•для логического сложения AvA=l.

Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.

6.Закон повторения:

     •для логического умножения: А&А=А;

•для логического сложения: AvA=A.

7. Законы операций с О и 1:

•для логического умножения: А&0 = 0;А&1=А;

•для логического сложения:

8. Законы общей инверсии:

•для логического умножения: A&B = AvB;

•для логического сложения: AvB = A~&B.

---

Вопросы и задания

1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Дополняет ли презентация информацию, содержащуюся в тексте параграфа?

 2.Найдите дополнительную информацию об унарной, позиционных и непозиционных системах счисления. Чем они различаются? Приведите примеры.

3. Цифры каких систем счисления приведены на рис. 1.1?

4.Объясните, почему позиционные системы счисления с основаниями 5, 10, 12 и 20 называют системами счисления анатомического происхождения.

5.Как от свёрнутой формы записи десятичного числа перейти к его развёрнутой форме?

---

Самое главное

Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.

Основные логические операции, определённые над высказываниями: инверсия, конъюнкция, дизъюнкция.

Система счисления — это знаковая система, в которой приняты определённые правила записи чисел. Знаки, с помощью которых записываются числа (рис. 1.1), называются цифрами, а их совокупность — алфавитом системы счисления.