| |
 |
|
|
Урок 7
Использование графов при решении задач Ключевые слова: Графы удобно использовать при решении некоторых классов задач. 1.3.3. Использование графов при решении задач Пример 1. Для того чтобы записать все трёхзначные числа, состоящие из цифр 1 и 2, можно воспользоваться графом (деревом) на рис. 1.7.
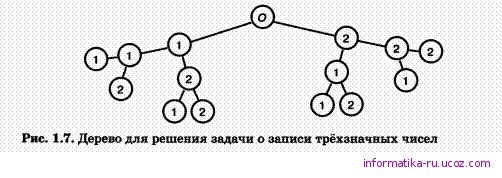
Дерево можно не строить, если не требуется выписывать все возможные варианты, а нужно просто указать их количество. В этом случае рассуждать нужно так: в разряде сотен может быть любая из цифр 1 и 2, в разряде десятков — те же два варианта, в разряде единиц — те же два варианта. Следовательно, число различных вариантов: 2-2-2 = 8. В общем случае, если известно количество возможных вариантов выбора на каждом шаге построения графа, то для вычисления общего количества вариантов нужно все эти числа перемножить. Пример 2. Рассмотрим несколько видоизменённую классическую задачу о переправе. На берегу реки стоит крестьянин (К) с лодкой, а рядом с ним — собака (С), лиса (Л) и гусь (Г). Крестьянин должен переправиться сам и перевезти собаку, лису и гуся на другой берег. Однако в лодку кроме крестьянина помещается либо только собака, либо только лиса, либо только гусь. Оставлять же собаку с лисой или лису с гусем без присмотра крестьянина нельзя — собака представляет опасность для лисы, а лиса — для гуся. Как крестьянин должен организовать переправу? 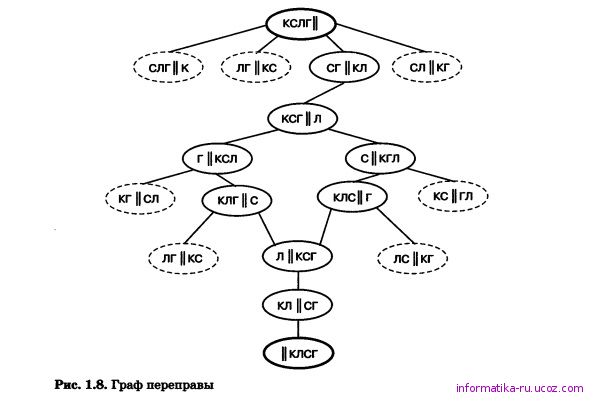Для решения этой задачи составим граф, вершинами которого будут исходное размещение персонажей на берегу реки, а также всевозможные промежуточные состояния, достигаемые из предыдущих за один шаг переправы. Каждую вершину-состояние переправы обозначим овалом и свяжем рёбрами с состояниями, образованными из неё (рис. 1.8). Недопустимые по условию задачи состояния выделены пунктирной линией; они исключаются из дальнейшего рассмотрения. Начальное и конечное состояния переправы выделены жирной линией. На графе видно, что существуют два решения этой задачи. Приведём соответствующий одному из них план переправы:
Пример 3. Рассмотрим следующую игру: сначала в кучке лежат 5 спичек; два игрока убирают спички по очереди, причём за 1 ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке 1 спичку. Выясним, кто выигрывает при правильной игре — первый (I) или второй (II) игрок. Игрок I может убрать одну спичку (в этом случае их останется 4) или сразу 2 (в этом случае их останется 3). Если игрок I оставил 4 спички, игрок П может своим ходом оставить 3 или 2 спички. Если же после хода первого игрока осталось 3 спички, второй игрок может выиграть, взяв две спички и оставив одну. Если после игрока II осталось 3 или 2 спички, то игрок I в каждой из этих ситуаций имеет шанс на выигрыш. Таким образом, при правильной стратегии игры всегда выиграет первый игрок. Для этого своим первым ходом он должен взять одну спичку. . На рис. 1.9 представлен граф, называемый деревом игры; на нём отражены все возможные варианты, в том числе ошибочные (проигрышные) ходы игроков.
Вопросы и задания 1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию? Самое главное В графических информационных моделях для наглядного отображения объектов используются условные графические изображения (образные элементы), зачастую дополняемые числами, символами и текстами (знаковыми элементами). Примерами графических моделей могут служить всевозможные схемы, карты, чертежи, графики и диаграммы, графы. Граф состоит из вершин, связанных линиями — рёбрами. Граф называется взвешенным, если его вершины или рёбра характеризуются некоторой дополнительной информацией — весами вершин (рёбер). Граф иерархической системы называется деревом. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь. |
|
