Логические элементы компьютера
Логические элементы компьютера — это электронные схемы с одним или несколькими входами и одним выходом, через которые проходят электрические сигналы, представляющие цифры 0 и 1.
Для реализации любых логических операций достаточно элементов трёх типов:
- Элемент НЕ (инвертор). Имеет один вход и один выход. Если на его вход Х поступает сигнал 0, то на выходе Z появится сигнал 1, а если на входе 1, то на выходе 0.
- Элемент И (конъюнктор). На его выходе Z сигнал 1 будет сформирован тогда и только тогда, когда сигнал 1 будет и на первом, и на втором входе. Если хотя бы на одном из входов будет 0, то и на выходе также будет 0.
- Элемент ИЛИ (дизъюнктор). Сигнал 1 на выходе будет получен, если
сигнал 1 поступает хотя бы на один вход: либо на Х, либо на Y, либо и на Х, и на Y одновременно. Сигнал 0 на выходе элемента ИЛИ появляется только в том случае, если сигнал 1 не поступил ни на один вход.
Простейшие элементы
В компьютерах все вычисления производятся с помощью логических элементов - электронных схем, выполняющих логические операции. Обозначения простейших элементов приводятся в таблице. Заметьте, что небольшой кружок на выходе (или на входе) обозначает операцию
«НЕ» (отрицание, инверсию).

Рис.1
Может показаться, что для реализации сложных логических функций нужно много разных видов логических элементов. Любую логическую функцию можно представить с помощью операций «НЕ», «И» и «ИЛИ» (такой набор элементов называется полным). Именно эта классическая «тройка» используется в книгах по логике, а также во всех языках программирования. Тем не менее инженеры часто предпочитают строить логические схемы на основе элементов «ИЛИ-НЕ».
Функция (штрих Шеффера) позволяет реализовать операции «НЕ», «И» и «ИЛИ», а значит, и любую другую операцию.
Если нужно составить схему по известному логическому выражению, её начинают строить с конца. Находят операцию, которая будет выполняться последней, и ставят на выходе соответствующий логический элемент. Затем повторяют то же самое для сигналов, поступающих на вход этого элемента. В конце концов должны остаться только исходные сигналы - переменные в логическом выражении.
Составим схему, соответствующую выражению
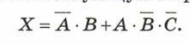
Последняя операция - это логическое сложение , поэтому на выходе схемы будет стоять элемент «ИЛИ»
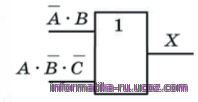
Рис.2
Для того чтобы получить на первом входе А В, нужно умно- жить А на В, поэтому добавляем элемент «И»
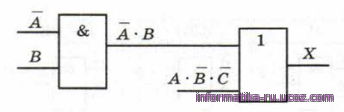
Рис.3
Чтобы получить А, ставим элемент «НЕ
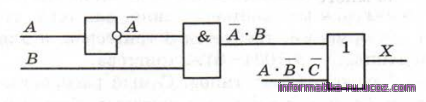
Рис.4
Аналогично разбираем вторую ветку, которая поступает на второй вход элемента «ИЛИ
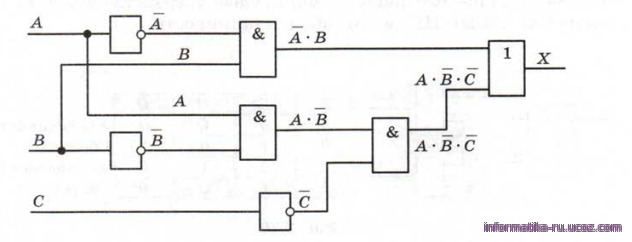
Рис.5
Схема составлена, её входами являются исходные сигналы А, В и С, а выходом - Х.
Триггер
Так называют электронную схему, которая может находиться только в двух состояниях (их можно обозначить как 0 и 1) и способна почти мгновенно переходить из одного состояния в другое. Триггер изобрели независимо друг от друга М. А. Бонч-Бруевич и англичане У. Икклз и Ф. Джордан в 1918 г.
В современных компьютерах на основе триггеров строится быстродействующая оперативная память. Один триггер способен хранить один бит данных.
Соответственно , для того, чтобы запомнить 1 байт информации, требуется 8 триггеров, а для хранения 1 килобайта данных — 8•1024 = 8192 триггера.
Триггеры бывают разных типов. Самый распространённый - это RS-триггер. Он имеет два входа, которые обозначаются как S (англ. set — установить) и R (англ. reset — сброс), и два выхода — Q и Q, причём выходной сигнал Q является логическим отрицанием сигнала Q (если @ - 1, то Q — 0, и наоборот).
RS-триггер можно построить на двух элементах «И-НЕ» или на двух элементах
«ИЛИ-НЕ». Условное обозначение RS-триггера, внутреннее устройство триггера на элементах «ИЛИ-НЕ» и его таблица истинности.
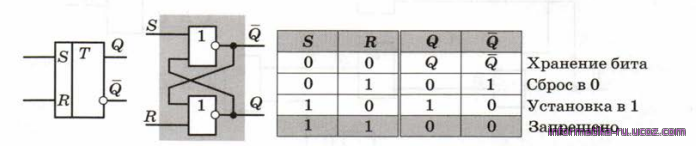
Рис.6
Триггер использует так называемые обратные связи - сигналы с выходов схем
«ИЛИ-НЕ» поступают на вход соседней схемы. Именно это позволяет хранить информацию.
Построим таблицу истинности триггера. Начнем с варианта, когда S = 0 и R = 1. Элемент «ИЛИ-НЕ» в нижней части схемы можно заменить на последовательное соединение элементов «ИЛИ» и «НЕ». Независимо от второго входа, на выходе
«ИЛИ» будет 1, а на выходе «НЕ» — ноль. Это значит, что Q = 0
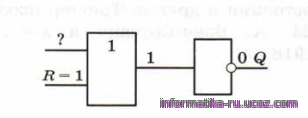
Рис.7
Тогда на входе другого элемента «ИЛИ-НЕ» будут два нуля,
а на выходе Q — единица
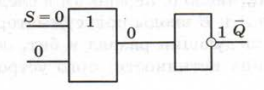
Рис.8
Поскольку основным выходом считается Q, мы записали в триггер значение 0. Схема симметрична, поэтому легко догадаться, что при S = 1 и R — 0 мы запишем в триггер 1 (Q - 1).
Теперь рассмотрим случай, когда S - 0 и R = 0. На входе первого элемента «ИЛИ» будет сигнал Q + 0 = Q, поэтому на выходе
- останется его предыдущее значение
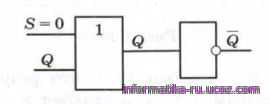
Рис.9
Аналогично легко показать, что на выходе @ тоже остаётся его предыдущее значение. Это режим хранения бита.
Для случая S = 1 и R - 1 мы увидим, что оба выхода становятся равны нулю - в этом нет смысла, поэтому такой вариант запрещён.
Для хранения многоразрядных данных триггеры объединяются в единый блок, который называется регистром. Регистры (размером от 8 до 64 битов) используются во всех процессорах для временного хранения промежуточных результатов.
Над регистром, как над единым целым, можно производить ряд стандартных операций: сбрасывать (обнулять), заносить в него код и т. д. Часто регистры способны не просто хранить информацию, но и обрабатывать её. Например, существуют регистры-счётчики, которые подсчитывают количество импульсов, поступающих на вход.
Сумматор
Как следует из названия, сумматор предназначен для сложения (суммирования) двоичных чисел. Сначала рассмотрим более простой элемент, который называют полусумматором. Он выполняет сложение двух битов с учетом того, что в результате может получиться двухразрядное число (с переносом в следующий разряд).
Обозначим через А и В входы полусумматора, а через Р и S выходы (перенос в следующий разряд и бит, остающийся в текущем разряде). Таблица истинности этого устройства показана
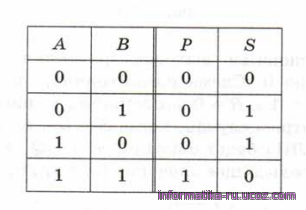
Рис.10
Легко увидеть, что столбец Р — это результат применения операции «И» ко входам А и В, а столбец S — результат операции «исключающее ИЛИ»:

Формулу для S можно также записать в таком виде:
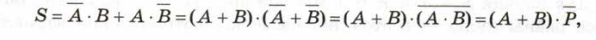
что позволяет построить полусумматор, используя всего четыре простейших элемента
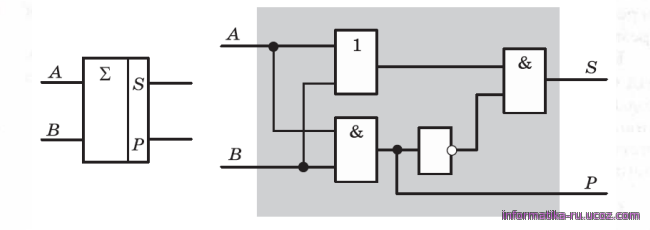
Рис.11
Логические функции для выходов сумматора вы можете найти самостоятельно.
Сумматор можно построить с помощью двух полусумматоров и одного элемента «ИЛИ».
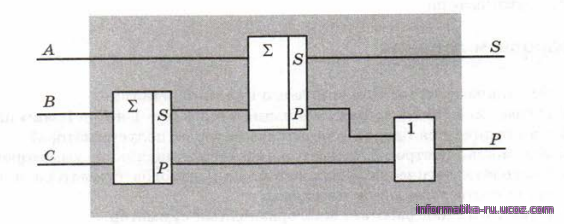
Рис.12







