Логические функции и логические выражения

Теория:

Реляционный подход организации баз данных, предложенный в 70-х годах XX века Э. Коддом, основывается на математической теории множеств и математической логике. Использование базы данных предполагает манипулирование данными, включающее в себя поиск необходимых данных. Именно здесь применяются реляционная алгебра и реляционное исчисление, предполагающее вычисление предикатов первого порядка.

Предикат — утверждение, высказанное об объекте.

Утверждение может иметь всего два значения: быть истинным или ложным. Принято считать, что истинное высказывание =1, а ложное =0. Поиск условий, при котором выражение становится истинным, — одна из задач манипулирования данными в БД.
Учитывая, что логические переменные могут принимать только два значения, у нас есть возможность привести полную таблицу значений логической функции в зависимости от логической операции и значений логических переменных, т. е. задать логическую функцию таблично.
Напомним, что основных (базовых) логических операций — три. Это конъюнкция — логическое умножение (обозначается ∧ или значком ∗, или не обозначается совсем), дизъюнкция — логическое сложение (обозначается ∨ или значком +) и инверсия — логическое отрицание (обозначается ¬ или чертой над логической переменной). Остальные операции выражаются через базовые.
Приведём таблицы истинности базовых операций, другими словами, таблицы значений логических функций в зависимости от значений логических переменных.

 

A B A∧B 0 0 0 0 1 0 1 0 0 1 1 1

A B A∨B 0 0 0 0 1 1 1 0 1 1 1 1

A ¬A 0 1 1 0

 

И для справки: ещё две операции, на которые часто обращают внимание в тестированиях и экзаменах.

Импликация A→B и эквиваленция A≡B.

 

A B A→B 0 0 1 0 1 1 1 0 0 1 1 1

A B A≡B 0 0 1 0 1 0 1 0 0 1 1 1

 

Импликация и эквиваленция выражаются через базовые операции.

 

A→B = ¬A∨B;

A≡B = A∧B∨¬A∧¬B.

 

Поиск в БД формулируется в виде словесного запроса, оборота речи, которому можно поставить в соответствие логическую операцию.

 

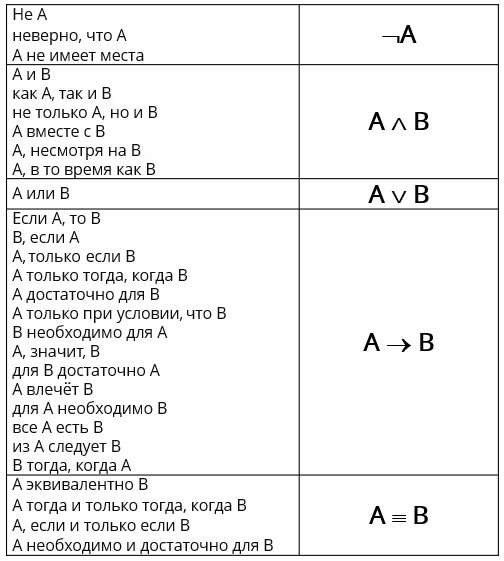
Рис. 1. Логические операции

 

Логическая функция - это функция, которая устанавливает соответствие между одним или несколькими высказываниями, которые называются аргументами функции, и высказыванием которое называется значением функции.

Это определение почти не отличается от определения числовой функции. Разница лишь та, что аргументом и значением числовой функции являются числа, а аргументом логической функции - высказывания.

Как можно составить логическую функцию? Очень просто.

Приведем пример: Пусть дано высказывание А. Оно может быть либо истинно, либо ложно. Определим высказывание В следующим образом: пусть В истинно, когда А ложно, и ложно когда А истинно.

Мы только что установили соответствие между высказыванием А и высказыванием В. Другими словами мы составили логическую функцию, аргументом которой является высказывание А и результатом высказывание В.

Функция, определённая таким образом, называется отрицанием и записывается так: ¬A . Читается так: не А.

Определим логические функции:

1. Инверсия (отрицание) — это логическое не. Говорят, что имея суждение А, можно образовать новое суждение, которое читается как «не А» или «неверно, что А». Для обозначения отрицания суждения употребляется символ ¬ или – над переменной. Запись ¬А читается как «не А»

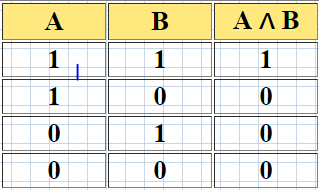
      2. Коньюкция - это логическое умножение. Обозначение: А & В ( АВ, А ∧ В ) . Читается так “ А и В “.

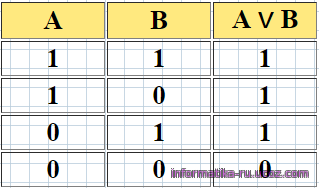
     3. Дизьюкция - это логическое сложение. Обозначение: А ∨ В , ( А + В ). Читается так: “ А или В ”.

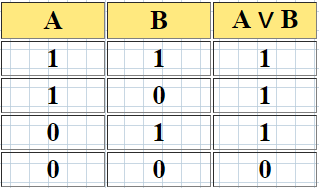
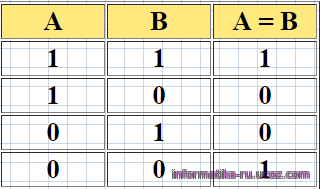
    4. Эквиваленция - это функция тождества. Она обозначается символами = , ~ , или <=>. Выбираем обозначение
А = В. («тогда и только тогда»). Запись А = В читается как «А эквивалентно В».

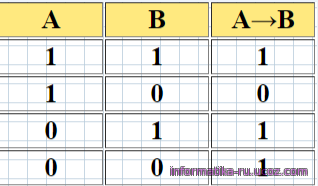
    5.Импликация - это логическое следование. Импликация двух высказываний А и В соответствует союзу «ЕСЛИ…ТО». Она обозначается символом →. Читается как «из А следует В». Обозначение: A→B.

Пример:

предположим, что перевозки осуществляются двумя компаниями — Pegasus и Quick. При этом Pegasus зарезервировал время отправления поездов в интервале [5:00;17:00], Quick — в интервале [14:00;23:00]. Необходимо выбрать временной интервал для поездов компании Alternative, такой, чтобы исключить интервалы, в которые одновременно ходят поезда Pegasus и Quick
Составим логическое выражение, заменив Pegasus и Quick на P и Q, а Alternative — на A. Выражение x∈P обозначает, что время отправления поезда зарезервировано компанией Pegasus.

Получим правило: ¬((x∈P)∧(x∈Q))→(x∈A)=1 при любом значении переменной x.

Преобразуем исходное выражение, заменив x∈P на P.

Получим: ¬(P∧Q)→A=1.

Заменим импликацию по правилу, приведённому выше: (P∧Q)∨A=1.

Т. е. временной интервал, в течение которого курсируют поезда компаний Pegasus и Quick, вместе с временным интервалом, когда курсируют поезда компании Alternative, перекрывают весь интервал движения поездов.
(P∧Q) — интервал [14:00;17:00], тогда A — интервалы [00:00;14:00] и [17:00;24:00].