Измерение информации

Любая наука рано или поздно приходит к необходимости как-то измерять то, что она изучает. Измерение информации это одна из важнейших задач теоретической информатики. Для человека информация это, прежде всего, смысл, заключённый в сигналах и данных. Как измерить смысл? На этот вопрос пока нет однозначного ответа.

Вспомним, что компьютеры не могут обрабатывать смысл, они работают только с данными (а не с информацией). При этом возникают чисто практические задачи: определить, сколько места займёт на диске текст, рисунок или видеофильм; сколько времени потребуется на передачу файла по компьютерной сети и т. п. По-этому чаще всего используется объёмный подход к измерению ин формации. Он заключается в том, что количество информации оце нивается просто по числу символов, используемых для её кодирования. С этой точки зрения стихотворение А. С. Пушкина и случайный набор букв могут содержать одинаковое количество ин формации. Конечно, такой подход не универсален, но он позволяет успешно решать практические задачи, связанные с компьютерной обработкой и хранением данных.

Что такое бит?

Рассмотрим электрическую лампочку, которая может находиться в двух состояниях: «горит» и «не горит». Тогда на вопрос «Горит ли сейчас лампочка» есть два возможных варианта ответа, которые можно обозначить цифрами 1 («горит») и 0 («не горит») (рис. 1.5). Поэтому ответ на этот вопрос (полученная информация) может быть записан как 0 или 11.

Цифры 0 и 1 называют двоичными, и с этим связано название единицы измерения количества информации бит. Английское слово bit - это сокращение от выражения binary digit «двоичная цифра. Впервые слово «бит» в этом значении использовал американский инженер и математик Клод Шеннон в 1948 г.

Бит - это количество информации, которую можно записать (закодировать) с помощью одной двоичной цифры.

 

 

 

 

 

 

 

 

 

Конечно, нужно договориться, что означают 0 и 1 (1 это «горит» или «не горит»?), но для измерения количества информации это не важно.

Например, в сообщении «подброшенная монета упала гербом» содержится 1 бит информации, потому что монета могла упасть гербом (обозначим это через 0) или «решкой» (1). Сообщение «Дверь открыта тоже содержит 1 бит, если считать, что дверь может быть в двух состояниях: открыта (0) или закрыта (1). Вот ещё пример диалога, в котором получена информация в 1 бит:

Вы будете чай или кофе?

Кофе, пожалуйста.

2 бита, 3 бита...

А если возможных вариантов не два, а больше? Понятно, что в этом случае количество информации будет больше, чем 1 бит. Представим себе, что на вокзале стоят 4 одинаковых поезда (рис. 1.6), причём только один из них проследует в Москву. Сколько битов понадобится для того, чтобы записать информацию о номере платформы, где стоит поезд на Москву?

Очевидно, что одного бита недостаточно, так как с помощью одной двоичной цифры можно закодировать только два варианта коды 0 и 1. А вот два бита дают как раз 4 разных сообщения: 00, 01, 10 и 11. Теперь нужно сопоставить эти коды номерам платформ, например, так: 100,2-01,310,4-11. Тогда сообщение 10 говорит о том, что поезд на Москву стоит на плат форме № 3. Это сообщение несёт 2 бита информации. Три бита дают уже 8 вариантов: 000, 001, 010, 011, 100, 101, 110 и 111. Таким образом, каждый бит, добавленный в сообщение, увеличивает количество вариантов в 2 раза (табл. 1.1).

 

 

 

 

 

 

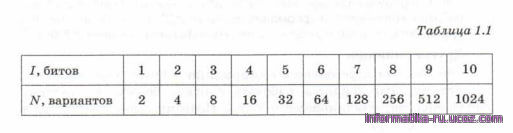
Наверно, вы заметили, что все числа в нижней строчке таблицы это степени числа 2: N = 2^i.

Осталось выяснить, чему равно количество информации, если выбор делается, скажем, из 5 возможных вариантов (или из любого количества, не являющегося степенью числа 2). С точки зрения приведённого выше рассуждения случаи выбора на 5, 6, 7 и 8 вариантов не различаются для кодирования двух двоичных цифр мало, а трёх достаточно. Поэтому использование трёх би тов для кодирования одного ва 5 возможных вариантов избыточно, ведь три бита позволяют закодировать целых 8 вариантов! Значит, выбор на 5 вариантов даёт меньше трёх битов информации.

Чтобы количественно измерить разницу между, скажем, 5 и 8 вариантами, придется допустить, что количество информации в битах может быть дробным числом. При этом информация, по-лученная при выборе из 5 вариантов, больше, чем 2 бита, но меньше, чем 3 бита. Точную формулу для ее вычисления получил в 1928 г. американский инженер Ральф Хартли. Эта формула ис пользует понятие логарифма, поэтому мы познакомимся с ней в 11 классе.

Тем не менее уже сейчас вы можете оценить количество информации при выборе из 5 вариантов. Допустим, на завтрак в лагере отдыха каждый день дают кашу одного из 5 видов. Чтобы закодировать вид каши, которую дают в понедельник, нужно, как мы знаем, 3 бита. Но меню на два дня может быть составлено 25 разными способами (5-5), поэтому для его кодирования достаточно 5 битов, ведь 25 < 32 = 2 ^ 5 * t Тогда получается, что количество информации при вы из 5 вариантов меньше, чем 5/2 = 2.5 Но и эту оценку можно уточнить трёх дней получаем 5 * 5 * 5 = 125 вариантов. Так как 125 < 128 = 2^7 количество информации при выборе из 5 вариантов составляет не больше, чем 7/3 = 2, 33 бита. И так да лее. Попробуйте самостоятельно показать, что при выборе из 5 ва риантов количество информации больше 2,25 бита. Верно ли, что при выборе из 6 вариантов количество информации менее 2,5 бита?

Другие единицы

Считать большие объёмы информации в битах неудобно хотя бы потому, что придётся работать с очень большими числами (миллиардами, триллионами и т. д.). Поэтому стоит ввести более крупные единицы.

1 байт = 8 битов.

Сразу возникает вопрос: а почему не 10 битов? Дело в том, что слово «байт» (англ. byte) имеет второе значение так назы вают наименьший блок (ячейку) памяти, который процессор ком пьютера может считать и обработать за один раз. Для современ ных компьютеров он состоит из 8 элементов, каждый из которых хранит 1 бит данных. Это связано с тем, что до недавнего времени при обработке текста использовался набор из 256 символов, так что для кодирования каждого символа было нужно 8 битов.

Объёмы данных, с которыми работают компьютеры, нередко намеряются миллионами и миллиардами байтов. В таких случаях используют единицы, образованные с помощью приставок:

1 Кбайт (килобайт) 1024 байта = 2^10 байта = 2^13 битов.

1 Мбайт (мегабайт) 1024 Кбайт 210 Кбайт = 2^20 байтов = 2^23 битов.

1 Гбайт (гигабайт) 1024 Мбайт.

1 Тбайт (терабайт) = 1024 Гбайт.