Урок №23. Законы алгебры логики.

1. УПРОЩЕНИЕ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ.

Для упрощения логических выражений применяют эквивалентные преобразования. Это означает, что исходное и упрощённое выражения определяют одну и ту же логическую функцию (имеют одинаковые таблицы истинности).

Законы алгебры логики, с помощью которых выполняют эквивалентные преобразования, формулируются для базовых логических операций — НЕ, И и ИЛИ (рис. 3.15).

Рис. 3.15

Закон двойного отрицания означает, что операция НЕ обратима: если применить её два раза, логическое значение не изменится. Закон исключённого третьего основан на том, что в классической (двузначной) логике любое логическое выражение либо истинно, либо ложно («третьего не дано»). Поэтому если А = 1, то А = 0 (и наоборот), так что произведение этих величин всегда равно нулю, а сумма — единице.

Операции с константами и закон повторения легко проверяются по таблицам истинности операций И и ИЛИ. Переместительный и сочетательный законы выглядят так же, как и в школьной математике. Нужно только помнить, что в логике 1 + 1 = 1, а не 2.

Распределительный закон для ИЛИ — это обычное раскрытие скобок. А вот для операции И мы видим незнакомое выражение, в алгебре это равенство неверно. Доказательство можно начать с правой части, раскрыв скобки:

(А + В)• (А + С) = А• А+А •С + В •А + В• С.

Дальше используем закон повторения (А • А = А) и заметим, что

А+А•С = А• (1 + С)=А•1=А.

Аналогично доказываем, что А + В • А = А • (1 + В) = А, таким образом,

(А + В) • (А + С) = А + В • С.

Равенство доказано. Попутно мы доказали также и закон поглощения для операции И (для ИЛИ вы можете сделать это самостоятельно). Отметим, что из распределительного закона следует полезная формула

А + ¬А • В = (А + ¬А) • (А + В) = А + В.

Правила, позволяющие раскрывать отрицание сложных выражений, названы в честь шотландского математика и логика Августа де Моргана. Обратите внимание, что при этом не просто «общее» отрицание переходит на отдельные выражения, но и операция И заменяется на ИЛИ (и наоборот). Доказать законы де Моргана можно с помощью таблиц истинности.

Теперь с помощью приведённых законов алгебры логики упростим логическое выражение  с тремя переменными:

А•В•¬С + ¬А•В•¬С = (А + ¬А)•В•¬С = В•¬С.

Здесь мы сначала вынесли общий множитель двух слагаемых за скобки, а затем применили закон исключённого третьего.

В общем случае можно рекомендовать такую последовательность действий:

1. Заменить все «небазовые» операции (исключающее ИЛИ, импликацию, эквиваленцию и др.) на их выражения через базовые операции НЕ, И и ИЛИ.
2. Раскрыть отрицания сложных выражений по законам де Моргана так, чтобы операции отрицания остались только у отдельных переменных.
3. Используя вынесение общих множителей за скобки, раскрытие скобок и другие законы алгебры логики, упростить выражение.

Пример

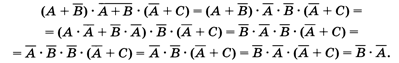
Здесь последовательно использованы закон де Моргана, распределительный закон, закон исключённого третьего, переместительный закон, закон повторения, снова переместительный закон и закон поглощения.

2. ОБУЧАЮЩИЙ ВИДЕОРОЛИК.

00:00

02:35