Алгебра в широком смысле этого слова — это наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами. Многие математические объекты (целые и рациональные числа, многочлены, векторы, множества) вы изучаете в школьном курсе алгебры, где знакомитесь с такими разделами математики, как алгебра чисел, алгебра многочленов, алгебра множеств и т. д.
Для информатики важен раздел математики, называемый алгеброй логики; объектами алгебры логики являются высказывания.
Высказывание — это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное.
Например, относительно предложений «Великий русский учёный М. В. Ломоносов родился в 1711 году» и «Two plus six is eight» можно однозначно сказать, что они истинны. Предложение «Зимой воробьи впадают в спячку» ложно. Следовательно, эти предложения являются высказываниями.
В русском языке высказывания выражаются повествовательными предложениями. Но не всякое повествовательное предложение является высказыванием.
Например, предложение «Это предложение является ложным» не является высказыванием, так как относительно него нельзя сказать, истинно оно или ложно, без того чтобы не получить противоречие. Действительно, если принять, что предложение истинно, то это противоречит сказанному. Если же принять, что предложение ложно, то отсюда следует, что оно истинно.
Относительно предложения «Компьютерная графика — самая интересная тема в курсе школьной информатики» также нельзя однозначно сказать, истинно оно или ложно. Подумайте сами почему.
Побудительные и вопросительные предложения высказываниями не являются.
Например, не являются высказываниями такие предложения, как «Запишите домашнее задание», «Как пройти в библиотеку?», «Кто к нам пришёл!».
Высказывания могут строиться с использованием знаков различных формальных языков — математики, физики, химии и т.д.
Примерами высказываний могут служить:
- «Na — металл» (истинное высказывание);
- «Второй закон Ньютона выражается формулой F = m • а» (истинное высказывание);
- «Периметр прямоугольника с длинами сторон а и b равен а • b» (ложное высказывание).
Не являются высказываниями числовые выражения, но из двух числовых выражений можно составить высказывание, соединив их знаками равенства или неравенства. Например:
- «3 + 5 = 2 • 4» (истинное высказывание);
- «II + VI > VIII» (ложное высказывание).
Не являются высказываниями и равенства или неравенства, содержащие переменные (предложения с переменными). Например, предложение «X < 12» становится высказыванием только при замене переменной каким-либо конкретным значением: «5 < 12» — истинное высказывание; «12 < 12» — ложное высказывание. Такие предложения с переменными иначе называют высказывательными формами.
Высказывательная форма — это повествовательное предложение, которое содержит хотя бы одну переменную и становится высказыванием, когда все переменные заменяются конкретными значениями.
Множество тех значений переменной, при которых получаются истинные высказывания, называют областью истинности высказывательной формы (предложения с переменной).
Все рассмотренные выше высказывания либо отражали отношения между двумя объектами, либо описывали некоторое свойство объекта. Такие высказывания называют простыми или элементарными.
Так, высказывание «Na — металл» описывает свойство («металл») объекта («Na»); высказывание «3 + 5 = 2 • 4» отражает отношение (« = ») между двумя объектами («3 + 5», «2 • 4»).
Из простых высказываний с помощью логических связок НЕ, И, ИЛИ можно строить составные высказывания.
Рассмотрим использование каждой логической связки отдельно.
Составное высказывание со связкой НЕ содержит одно простое высказывание. Составное высказывание со связкой НЕ истинно, если содержащееся в нём простое высказывание ложно.
Например, простое высказывание «Число 5 является чётным» ложно; составное высказывание «Число 5 НЕ является чётным» истинно.
Составное высказывание со связкой НЕ ложно, если содержащееся в нём простое высказывание истинно. Например, простое высказывание «Последняя буква в слове “логика” является гласной» истинно; составное высказывание «Последняя буква в слове “ логик а” НЕ является гласной» ложно.
Работать со связкой НЕ достаточно сложно. В высказываниях на русском языке логическая связка НЕ ставится в середине высказывания, и не всегда бывает понятно, где именно её следует поставить. Например, в высказывании «Петя решил правильно все задания контрольной работы» для логической связки НЕ возможны такие места:
1) Петя НЕ решил правильно все задания контрольной работы.
2) Петя решил НЕправилъно все задания контрольной работы.
3) Петя решил правильно НЕ все задания контрольной работы.
Очевидно, второе из этих высказываний имеет совсем иной смысл, чем первое и третье.
По сути, с помощью логической связки НЕ мы строим отрицание исходного высказывания.
Отрицанием высказывания «У меня дома есть компьютер» будет высказывание «Неверно, что у меня дома есть компьютер» или, что в русском языке то же самое, «У меня дома нет компьютера ».
Отрицанием высказывания «Я не знаю китайский язык» будет высказывание «Неверно, что я не знаю китайский язык» или, что в русском языке то же самое, «Я знаю китайский язык».
Отрицанием высказывания «Все юноши 8-х классов — отличники» является высказывание «Неверно, что все юноши 8-х классов — отличники», другими словами, «Не все юноши 8-х классов — отличники».
Для того чтобы избежать двусмысленности при составлении высказываний со связкой НЕ, рекомендуется выбирать один из двух вариантов:
1) использовать речевой оборот «неверно, что» и всегда ставить его перед исходным высказыванием;
2) строить отрицание к сказуемому, добавляя к соответствующему глаголу частицу «не».
Сформулируйте отрицания высказываний «Последняя буква в слове “логика” является гласной», «Число 5 является чётным» с речевым оборотом «Неверно, что». Какой ещё вариант отрицания исходных высказываний вы можете предложить?
Составное высказывание со связкой И содержит два простых высказывания. Составное высказывание со связкой И истинно тогда и только тогда, когда истинны оба входящие в него простые высказывания.
Например, простые высказывания «Число 324 делится на 7», «Число 324 делится на 5» — оба ложны; простые высказывания «Число 324 делится на 3», «Число 324 делится на 2» — оба истинны. Рассмотрим образованные из них с помощью логической связки И составные высказывания:
1) «Число 324 делится на 7 И на 5» — ложное высказывание;
2) «Число 324 делится на 7 И на 3» — ложное высказывание;
3) «Число 324 делится на 7 И на 2» — ложное высказывание;
4) «Число 324 делится на 5 И на 3» — ложное высказывание;
5) «Число 324 делится на 5 И на 2» — ложное высказывание;
6) «Число 324 делится на 3 И на 2» — истинное высказывание.
Рассмотрите следующие высказывания: «Основоположником
алгебры логики является Джордж Буль», «Исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике», «Основоположником алгебры логики является Джордж Буль, и исследования Клода Шеннона позволили применить алгебру логики в вычислительной технике». Сделайте вывод об истинности третьего высказывания, предварительно выяснив с помощью Интернета истинность первых двух высказываний.
Составное высказывание со связкой ИЛИ содержит два простых высказывания. Составное высказывание со связкой ИЛИ ложно тогда и только тогда, когда ложны оба входящие в него простые высказывания.
Рассмотрим составные высказывания, образованные с помощью логической связки ИЛИ:
1) «Число 324 делится на 7 ИЛИ на 5» — ложное высказывание;
2) «Число 324 делится на 7 ИЛИ на 3» — истинное высказывание;
3) «Число 324 делится на 7 ИЛИ на 2» — истинное высказывание;
4) «Число 324 делится на 5 ИЛИ на 3» — истинное высказывание;
5) «Число 324 делится на 5 ИЛИ на 2» — истинное высказывание;
6) «Число 324 делится на 3 ИЛИ на 2» — истинное высказывание.
Рассмотрите следующие высказывания: «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу», «Лейбниц является основоположником бинарной арифметики», «Идея использования в логике математической символики принадлежит Готфриду Вильгельму Лейбницу, или Лейбниц является основоположником бинарной арифметики». Сделайте вывод об истинности третьего высказывания, предварительно выяснив с помощью Интернета истинность первых двух высказываний.
В обычной жизни связка ИЛИ зачастую трактуется в исключающем смысле. Вспомните, например, диагноз, который поставил лекарь Богомол Буратино: «Одно из двух: или пациент жив, или он умер». Что касается математической логики и программирования, то в них ИЛИ воспринимается в неисключающем смысле. Так, высказывание «Иван может перекусить бутербродом или яблоком» означает, что Иван может перекусить бутербродом или яблоком или и тем, и другим.
Составные высказывания можно строить не только из элементарных высказываний, но и из других составных высказываний.
Например: «В слове “вентиль” первая буква согласная И вторая — гласная, ИЛИ в слове “кулер” шесть букв» — истинное высказывание.
Операция НЕ часто называется отрицанием или инверсией. В алгебре логики всего два возможных значения (0 и 1), поэтому логическое отрицание — это переход от одного значения к другому: от 1 к 0 или наоборот. Если высказывание А истинно, то НЕ А ложно, и наоборот.
Используя дополнительные источники, переведите на русский язык слово inverse, от которого произошло слово «инверсия».
Операцию НЕ обозначают чертой сверху, например: Ā. В школьном алгоритмическом языке эта операция обозначается словом не, а в языке программирования Паскаль — английским словом not.
Используя дополнительные источники, найдите другие обозначения операции НЕ.
Операцию НЕ можно задать в виде таблицы (рис. 2.1).
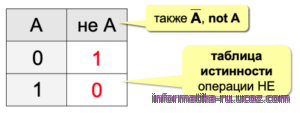
Эта таблица состоит из двух частей: слева перечисляются все возможные значения исходной величины (их всего два — 0 и 1), а в последнем столбце записывают результат выполнения логической операции для каждого из этих вариантов. Такая таблица называется таблицей истинности логической операции. Таблица истинности задаёт логическую функцию.
Логическая функция — это правило преобразования входных логических значений в логическое значение-результат.
Используя таблицу истинности на рис. 2.1, определите, как можно упростить выражение не(не А). Рассмотрите оба варианта: когда А = 0 и когда А = 1. Сделайте вывод.
Из двух простых высказываний А и B (например, А = Сейчас идёт дождь, В = Форточка открыта) можно составить сложное высказывание А и B. Высказывание А и В истинно в том и только в том случае, когда оба высказывания, А и Б, истинны одновременно.
Для понимания операции И можно представить себе простую схему, в которой для включения лампочки используются два выключателя, соединённых последовательно (рис. 2.2).
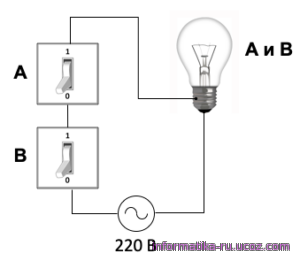
Чтобы лампочка загорелась, нужно обязательно включить оба выключателя. Вместе с тем, чтобы выключить лампочку, достаточно выключить любой из них.
Операция И (в отличие от НЕ) выполняется с двумя логическими значениями. В алгоритмическом языке системы КуМир операция И обозначается словом и, а в Паскале — словом and.
Используя дополнительные источники, найдите другие обозначения операции И.
В таблице истинности операции И будет уже не один столбец с исходными данными, а два, мы обозначим исходные данные как А и В. Число строк также выросло, с 2 до 4, поскольку с помощью 2 бит можно записать 4 разных комбинации значений двух переменных: 00, 01, 10 и 11. Как следует из определения операции И, в последнем столбце будет всего одна единица, для варианта А = В = 1 (оба высказывания, А и В, истинны одновременно) — рис. 2.3.
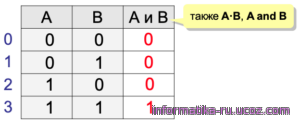
Из значений А и В в каждой строке этой таблицы составьте двоичное число и запишите его в десятичной системе счисления. Почему строки в таблице расположены именно так?
Легко проверить, что этот результат можно получить «обычным» умножением А на B, поэтому операцию И называют логическим умножением. Она часто обозначается знаком умножения (точкой): А • B.
С точки зрения обычной математики, эта операция выбирает наименьшее из исходных значений. Математики используют ещё одно название операции И — конъюнкция.
Используя дополнительные источники, выясните, от какого слова произошло слово «конъюнкция» и что оно обозначает.
С помощью таблицы истинности можно упрощать логические выражения. Например, рассмотрим выражение А и 1. По таблице истинности на рис. 2.3 получаем:
при А = 0: А и 1 = 0 и 1 = 0
при А = 1: А и 1 = 1 и 1 = 1.
Можно заметить, что в любом случае результат совпадает с А, поэтому А и 1 = А.
Используя таблицу истинности операции И, упростите выражения: а) А и 0; б) А и А; в) А и (не А).
Высказывание А или В (например, «Сейчас идет дождь или форточка открыта») истинно тогда, когда истинно хотя бы одно из входящих в него высказываний или оба одновременно.
В алгоритмическом языке операция ИЛИ обозначается словом или, а в языке Паскаль — английским словом or.
Используя дополнительные источники, найдите другие обозначения операции ИЛИ.
Для понимания операции ИЛИ можно представить себе схему с двумя выключателями, соединёнными параллельно (рис. 2.4).
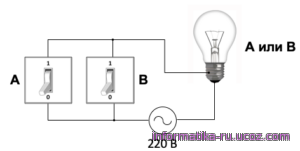
Чтобы лампочка загорелась, достаточно включить хотя бы один из выключателей. Чтобы выключить лампочку, необходимо обязательно выключить оба. В таблице истинности будет только один ноль — для варианта А = В = 0 (рис. 2.5).
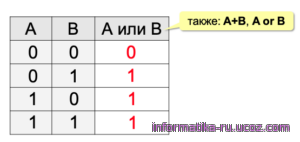
Операцию ИЛИ называют логическим сложением, потому что она похожа на обычное математическое сложение. Поэтому она часто обозначается знаком сложения: А+В. Единственное отличие — в последней строке таблицы истинности: в математике 1+1 равно 2, а в алгебре логики — единице.
Можно считать, что в результате применения операции ИЛИ из исходных значений выбирается наибольшее. Другое название этой операции — дизъюнкция.
Используя дополнительные источники, выясните, от какого слова произошло слово «дизъюнкция» и что оно обозначает.
Запишите в тетради ответы на следующие вопросы.
— Сколько строк в таблице истинности функции с двумя переменными?
— Сколько существует возможных вариантов распределения нулей и единиц в последнем столбце?
— Сколько можно придумать различных логических функций с двумя переменными?
Используя таблицу истинности операции ИЛИ, упростите выражения:
а) А или 0; б) А или 1; в) А или А; г) А или (не А).









