Таблицы и графы
Ключевые слова:
• схема
• карта
• чертёж
• график
• диаграмма
• граф
• сеть
• дерево
• таблица
1.3.1. Многообразие графических информационных моделей
В графических информационных моделях для наглядного отображения объектов используются условные графические изображения (образные элементы), зачастую дополняемые числами, символами и текстами (знаковыми элементами). Примерами графических моделей могут служить всевозможные схемы, карты, чертежи, графики и диаграммы.
Схема — это представление некоторого объекта в общих, главных чертах с помощью условных обозначений. С помощью схем может быть представлен и внешний вид объекта, и его структура. Схема как информационная модель не претендует на полноту предоставления информации об объекте. С помощью особых приёмов и графических обозначений на ней более рельефно выделяется один или несколько признаков рассматриваемого объекта. Примеры схем приведены на рис. 1.5.
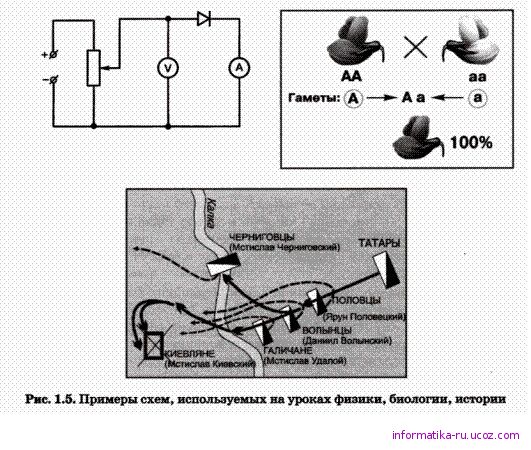
Уменьшенное обобщённое изображение поверхности Земли на плоскости в той или иной системе условных обозначений даёт нам географическая карта.
Чертёж — условное графическое изображение предмета с точным соотношением его размеров, получаемое методом проецирования. Чертёж содержит изображения, размерные числа, текст. Изображения дают представления о геометрической форме объекта, числа — о величине объекта и его частей, надписи — о названии, масштабе, в котором выполнены изображения.
График — графическое изображение, дающее наглядное представление о характере зависимости одной величины (например, пути) от другой (например, времени). График позволяет отслеживать динамику изменения данных.
Диаграмма — графическое изображение, дающее наглядное представление о соотношении каких-либо величин или нескольких значений одной величины, об изменении их значений. Более подробно типы диаграмм и способы их построения будут рассмотрены при изучении электронных таблиц.
1.3.2. Графы
Если объекты некоторой системы изобразить вершинами, а связи между ними — линиями (рёбрами), то мы получим информационную модель рассматриваемой системы в форме графа. Вершины графа могут изображаться кругами, овалами, точками, прямоугольниками и т. д.
Граф называется взвешенным, если его вершины или рёбра характеризуются некоторой дополнительной информацией — весами вершин или рёбер.
На рис. 1.6 с помощью взвешенного графа изображены дороги между пятью населёнными пунктами А, В, С, D, Е; веса рёбер — протяжённость дорог в километрах.

Путь по вершинам и рёбрам графа, в который любое ребро графа входит не более одного раза, называется цепью. Цепь, начальная и конечная
вершины которой совпадают, называется циклом.
Граф с циклом называется сетью. Если героев некоторого литературного произведения представить вершинами графа, а существующие между ними связи изобразить рёбрами, то мы получим граф, называемый семантической сетью.
Графы как информационные модели находят широкое применение во многих сферах нашей жизни. Например, можно существующие или вновь проектируемые дома, сооружения, кварталы изображать вершинами, а соединяющие их дороги, инженерные сети, линии электропередач и т. п. — рёбрами графа. По таким графам можно планировать оптимальные транспортные маршруты, кратчайшие объездные пути, расположение торговых точек и других объектов.
Дерево — это граф, в котором нет циклов, т. е. в нём нельзя из некоторой вершины пройти по нескольким различным рёбрам и вернуться в ту же вершину. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь.
Всякая иерархическая система может быть представлена с помощью дерева. У дерева выделяется одна главная вершина, называемая его корнем. Каждая вершина дерева (кроме корня) имеет только одного предка, обозначенный предком объект входит в один класс высшего уровня. Любая вершина дерева может порождать несколько потомков — вершин, соответствующих классам нижнего уровня. Такой принцип связи называется «один-ко-многим». Вершины, не имеющие порождённых вершин, называются листьями.
Родственные связи между членами семьи удобно изображать с помощью графа, называемого генеалогическим или родословным деревом.
1.3.3. Использование графов при решении задач
Пример 1. Для того чтобы записать все трёхзначные числа, состоящие из цифр 1 и 2, можно воспользоваться графом (деревом) на рис. 1.7.
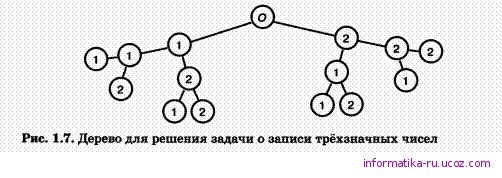
Дерево можно не строить, если не требуется выписывать все возможные варианты, а нужно просто указать их количество. В этом случае рассуждать нужно так: в разряде сотен может быть любая из цифр 1 и 2, в разряде десятков — те же два варианта, в разряде единиц — те же два варианта. Следовательно, число различных вариантов: 2-2-2 = 8.
В общем случае, если известно количество возможных вариантов выбора на каждом шаге построения графа, то для вычисления общего количества вариантов нужно все эти числа перемножить.
Табличные информационные модели
В табличных информационных моделях информация об объектах представляется в виде прямоугольной таблицы, состоящей из столбцов и строк.
Вам хорошо известно табличное представление расписания уроков, в табличной форме представляются расписания движения автобусов, самолётов, поездов и многое другое.
Представленная в таблице информация наглядна, компактна и легко обозрима.
1.4.1. Представление данных в табличной форме
В качестве информационных моделей объектов, обладающих одинаковыми наборами свойств, как правило, используются таблицы типа «объект—свойство».
Например, информацию о регионах нашей страны можно представить с помощью таблицы, фрагмент которой приведён в табл. 1.1.
В этой таблице каждая строка содержит информацию об одном объекте — регионе;
столбцы — отдельные характеристики (свойства) рассматриваемых объектов: название, дата образования, площадь и т. д. Т
В этой таблице отражена связь «количество пропущенных уроков» между объектами класса «Учащиеся» и объектами класса «Число».
Табличные информационные модели
В таблице «Расстояния между городами» (табл. 1.3) представлены расстояния между парами объектов, принадлежащих одному классу «Город».
Создайте эту таблицу в текстовом редакторе и добавьте в свободные строку и столбец информацию о своём населённом пункте.
Таблица 1.3
Расстояния между городами (км)
| Город | Город | ||||
|---|---|---|---|---|---|
| Москва | Петрозаводск | Самара | Казань | ||
| Москва | 1076 | 1009 | 815 | ||
| Петрозаводск | 1076 | 2145 | 1891 | ||
| Самара | 2145 | 631 | |||
| Казань | 815 | 1891 | 631 | ||
В форме таблицы «объект—объект» можно представить информацию о наличии границ
(сухопутной, морской, озёрной, речной) России с другими странами; её фрагмент представлен в табл. 1.4.
Граница Российской Федерации
| Страна | Граница | |||
|---|---|---|---|---|
| Сухопутная | Речная | Озерная | Морская | |
| Норвегия | 1 | 1 | 0 | 1 |
| Финляндия | 1 | 1 | 1 | 1 |
| Латвия | 1 | 1 | 1 | 0 |
| Корея | 0 | 1 | 0 | 1 |
| Япония | 0 | 0 | 0 | 0 |
Если граница соответствующего вида есть, то в нужную ячейку ставится 1, а если нет — О.
Важная особенность этой таблицы состоит в том, что в ней фиксируются не количественные («Сколько?»), а качественные свойства (наличие/отсутствие связи между объектами).
Табличные информационные модели
1.4.2. Использование таблиц при решении задач
Рассмотрим несколько примеров задач, которые удобно решать с помощью табличных информационных моделей.
Пример 1. Два игрока играют в следующую игру. Перед ними лежат две кучи камней, в первой из которых 3 камня, а во второй 2 камня.У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 1 камень в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 16. Кто выигрывает при безошибочной игре — игрок, делающий первый ход, или игрок, де
лающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
Табличные информационные модели
Три числа в каждой ячейке таблицы обозначают соответственно количество камней в кучах и их сумму. В первом столбце зафиксировано распределение камней перед игрой (исходное положение).
Во втором столбце рассмотрены все возможные варианты ходов первого игрока; победить с первого хода он не может.
В третьем столбце рассмотрены имеющиеся выигрышные варианты ходов второго игрока (отмечены «галочкой»). При безошибочной игре первого игрока такие ситуации возникнуть не должны. Поэтому рассматриваем все возможные ходы второго игрока в случаях, когда у него нет выигрышного хода. Если получены одинаковые варианты, то все из них, кроме одного, исключаем из дальнейшего рассмотрения.
В четвёртом столбце отмечены имеющиеся выигрышные варианты второго хода первого игрока. При безошибочной игре второго игрока такие ситуации возникнуть не должны. Поэтому рассматриваем все возможные ходы первого игрока в случае, когда у него нет выигрышного хода.
В пятом столбце отмечены выигрышные ходы второго игрока, имеющиеся при всех вариантах хода первого игрока
Таким образом, при безошибочной игре соперников побеждает второй игрок. Его первый ход должен быть таким, чтобы в кучах стало 4 и 3 камня.
Пример 2. С помощью взвешенного графа на рис. 1.6 представлена схема дорог, соединяющих населённые пункты А, В, С, D, Е. Построим таблицу, соответствующую этому графу (рис. 1.10).
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | X | 50 | 90 | ||
| B | 50 | X | 90 | ||
| C | 90 | X | 80 | 60 | |
| D | 80 | X | 70 | ||
| E | 90 | 60 | 70 | X |
Рис. 1.10. Весовая матрица
Если между парой населённых пунктов существует дорога, то в ячейку на пересечении соответствующих строки и столбца записывается число, равное её длине. Имеющиеся в таблице пустые клетки означают, что дорог между соответствующими населёнными пунктами нет. Построенная таким образом таблица называется весовой матрицей.
Глава 1. Моделирование и формализация
Для решения некоторых задач бывает удобно по имеющейся таблице строить граф. При этом одной и той же таблице могут соответствовать графы, внешне не похожие друг на друга. Например, рассмотренной выше таблице кроме графа на рис. 1.6 соответствует граф на рис.1.11.
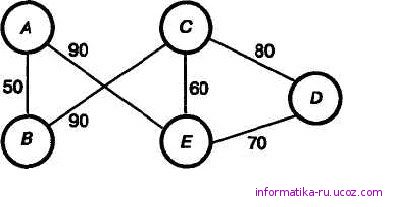
Рис. 1.11. Вариант графа, представляющего схему дорог
Пример 3. Таблицы типа «объект—объект» удобно использовать для решения логических задач, в которых требуется установить взаимно однозначное соответствие между объектами нескольких классов. Рассмотрим задачу, в которой объекты связаны тремя парами отношений.
Три подружки — Аня, Света и Настя — купили различные молочные коктейли в белом, голубом и зелёном стаканчиках. Ане достался не белый стаканчик, а Свете — не голубой. В белом стаканчике не банановый коктейль. В голубой стаканчик налит ванильный коктейль. Света не любит клубничный коктейль.
Требуется выяснить, какой коктейль и в каком стаканчике купила каждая из девочек.
Создадим три следующие таблицы:
| Стаканчик | Девочка | ||
|---|---|---|---|
| Аня | Света | Настя | |
| Белый | |||
| Голубой | |||
| Зеленый | |||
| Стаканчик | Коктейль | ||
| Банановый | Ванильный | Клубничный | |
| Белый | |||
| Голубой | |||
| Зеленый | |||
Табличные информационные модели
| Коктейль | Девочка | ||
|---|---|---|---|
| Аня | Света | Настя | |
| Банановый | |||
| Ванильный | |||
| Клубничный | |||
Отметим в таблицах информацию, содержащуюся в условии задачи:
| Стаканчик | Девочка | ||
|---|---|---|---|
| Аня | Света | Настя | |
| Белый | 0 | ||
| Голубой | 0 | ||
| Зеленый | |||
| Стаканчик | Коктейль | ||
| Банановый | Ванильный | Клубничный | |
| Белый | 0 | ||
| Голубой | 1 | ||
| Зеленый | |||
| Коктейль | Девочка | ||
|---|---|---|---|
| Аня | Света | Настя | |
| Банановый | |||
| Ванильный | |||
| Клубничный | 0 | ||
Имеющейся во второй таблице информации достаточно для того, чтобы заполнить всю эту таблицу:
| Стаканчик | Коктейль | ||
|---|---|---|---|
| Банановый | Ванильный | Клубничный | |
| Белый | 0 | 0 | 1 |
| Голубой | 0 | 1 | 0 |
| Зеленый | 1 | 0 | 0 |
Глава 1. Моделирование и формализация
Используя факты, что Света купила не клубничный коктейль и что этот коктейль был налит в белый стаканчик, заполняем всю первую таблицу:
| Стаканчик | Девочка | ||
|---|---|---|---|
| Аня | Света | Настя | |
| Белый | 0 | 0 | 1 |
| Голубой | 1 | 0 | 0 |
| Зеленый | 0 | 1 | 0 |








