1. ЧТО ТАКОЕ СИСТЕМА СЧИСЛЕНИЯ.
Система счисления — это правила записи чисел с помощью специальных знаков — цифр, а также правила выполнения операций с этими числами.
Первоначально люди считали на пальцах — это самый простой способ, который используется и сейчас. Один загнутый (или отогнутый) палец обозначал единицу (один день, одного человека, одного барана и т. п.). Такая система счисления называется унарной (от латинского слова unus — один). В качестве цифры можно использовать камешки, узелки, счётные палочки (как в начальной школе), зарубки на дереве (как Робинзон Крузо) или на кости, чёрточки и точки на бумаге, другие одинаковые знаки или предметы.
С помощью унарной системы можно записывать только натуральные числа, причём запись больших чисел получается очень длинной (представьте себе, как записать число «миллион»).
2. НЕПОЗИЦИОННАЯ СИСТЕМЫ СЧИСЛЕНИЯ.
Непозиционная система счисления — это такая система, в которой значение цифры не зависит от её места (позиции) в записи числа.
Например, цифра в любой позиции числа, записанного в унарной системе, всегда обозначает единицу, поэтому унарная система — одна из непозиционных систем счисления.
Непозиционную систему счисления использовали в Египте. Египтяне придумали 7 знаков-иероглифов, которые обозначали степени числа 10 (чёрточка, хомут, верёвка, гушка, человек) — рис. 2.11.
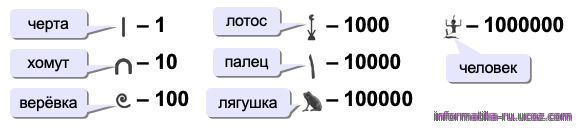
Рис. 2.11
Запишите в египетской системе число 647.
В римской системе (она также считается непозиционной) в качестве цифр используются латинские буквы: I обозначает 1, V — 5, X — 10, L — 50, С — 100, D — 500, М — 1000. Единицы, десятки, сотни и тысячи кодировались отдельными группами цифр, например:
2368 = 2000 + 300 + 60 + 8 =
= (1000 + 1000) + (100 + 100 + 100) +
+ (50 + 10) + (5 + 1 + 1 + 1) = MMCCCLXVIII
Больше трёх одинаковых цифр подряд не ставили, поэтому число 4 записывали как IV. Здесь меньшая цифра (I) стоит перед большей (V); такая запись означает вычитание меньшего числа из большего, т. е.
IV = 5 — 1 = 4.
Запишите в римской системе счисления числа 9, 40, 90, 400 и 900.
Запишите в римской системе счисления числа: 2323, 1786, 1944 и 3499.
У римской системы есть несколько серьёзных недостатков:
- можно записывать только натуральные числа (что делать с дробными и отрицательными?);
- чтобы записывать большие числа, необходимо вводить всё новые и новые цифры (иногда использовались цифры с подчёркиванием или чертой сверху, что обозначало увеличение в 1000 раз: V — 5000, X — 10000 и т. д.);
- сложно выполнять арифметические действия.
Запишите в римской системе числа 8494 и 12849.
Сейчас римская система применяется для нумерации веков (XXI век), глав в книгах, на циферблатах часов (например, на Спасской башне Московского Кремля).
В славянской системе счисления в качестве цифр использовались буквы алфавита, над которыми ставился знак («титло») — рис.2.12.

Если в ряд стояло несколько цифр, знак «титло» ставился только у второй с конца (предпоследней). Старшие цифры записывались справа от младших, например число 11 записывалось как  .
.
Используя Интернет, выясните, где находятся часы, на циферблате которых нанесены числа в славянской системе счисления.
Запишите числа 27, 58, 137 и 879 в славянской системе счисления.
3. ПОЗИЦИОННАЯ СИСТЕМА СЧИСЛЕНИЯ.
Позиционная система счисления — это такая система, в которой значение цифры полностью определяется её местом (позицией) в записи числа.
Пример позиционной системы счисления — привычная нам десятичная система. В числе 6375 цифра 6 обозначает тысячи (6000), цифра 3 — сотни (300), цифра 7 — десятки (70), а цифра 5 — единицы:
6375 = 6 • 1000 + 3 • 100 + 7 • 10 + 5 • 1
Алфавит системы счисления — это используемый в ней набор цифр.
Основание системы счисления — это количество цифр в алфавите (мощность алфавита).
В десятичной системе основание — 10, алфавит состоит из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Число 10, вероятно, было выбрано потому, что люди сначала использовали для счета свои 10 пальцев на руках.
Разряд — это позиция цифры в записи числа. Разряды в записи целых чисел нумеруются с нуля справа налево.
Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов, необходимых для записи любых чисел.
У позиционной системы счисления есть основание. Основание десятичной системы — число 10; степени основания определяют «веса» позиций (разрядов) в записи числа. Из двух одинаковых цифр, находящихся в записи числа рядом, левая цифра имеет в 10 раз большее значение, чем правая.
4. РАЗВЕРНУТАЯ ФОРМА ЗАПИСИ ЧИСЛА.
Существует множество позиционных систем счисления. Позиционная система счисления определяется основанием, в качестве которого можно использовать произвольное целое число q > 1. Алфавитом позиционной системы счисления с основанием q служат числа 0, 1, q — 1, каждое из которых может быть записано с помощью одного уникального символа; младшей цифрой всегда является 0.
В позиционной системе счисления с основанием q любое неотрицательное целое число может быть представлено в виде
Aq = an-1 • qn-1 + an-2 • qn-2 + a0 • q0 (1)
Здесь:
А — число;
q — основание системы счисления;
аi — цифры, принадлежащие алфавиту данной системы счисления;
n— количество разрядов числа;
qi — «вес» i-ro разряда.
Запись числа по формуле (1) называется развёрнутой формой записи. Свёрнутой формой записи числа называется его представление в виде an-1 an-2 … a1a2
Пример:
Рассмотрим десятичное число 4351. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме переходим к развёрнутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:
4 • 103 + 3*102+5*101+1* 10°.
Чтобы перевести число из позиционной системы счисления с основанием q в десятичную систему счисления, необходимо записать исходное число в развёрнутой форме и вычислить значение получившегося арифметического выражения.
Пример:
Переведём в десятичную систему счисления число 14235, представленное в системе счисления с основанием 5.
Построим развёрнутую запись числа 14235:
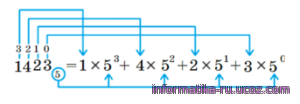
Вычислим значение выражения:
1 • 53 + 4 • 52 + 2 • 51 + 3 • 5° = 125 + 100 + 10 + 3 = 238.
Итак, 14235 = 23810.









