1. ЛОГИЧЕСКИЕ УРАВНЕНИЯ

Если приравнять два логических выражения, мы получим уравнение. Его решением будут значения переменных, при которых уравнение превращается в истинное равенство, т. е. когда значения левой и правой частей совпадают. Например, уравнение А • В = 1 имеет единственное решение: А = В = 1, для остальных комбинаций значений переменных левая часть равна нулю. В то же время уравнение А + В = 1 имеет три решения: (А = 0, В = 1), (А = 1, В = 0) и А = В = 1.

Логическое уравнение всегда имеет конечное количество решений. Для уравнения с n переменными количество решений не может быть больше, чем количество комбинаций n двоичных значений, равное 2ⁿ.

2. ВСЕ РЕШЕНИЯ УРАВНЕНИЯ.

Пример 1. 

Требуется найти все решения уравнения

Способ 1. Вспоминаем, что импликация равна нулю только тогда, когда первое выражение равно 1, а второе — 0. Поэтому исходное уравнение сразу разбивается на два:

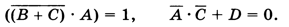
Первое уравнение помощью закона де Моргана можно преобразовать к виду ¬В• ¬С • А = 1, откуда сразу следует, что все три сомножителя должны быть равны 1. Это значит, что A=1, B=0  и С = 0. Кроме того, из второго уравнения следует, что D=0. Решение найдено, причем оно единственное.

Способ 2. Заменяя импликацию по формуле A→B=¬A+B, получаем

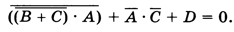
Используя закон де Моргана:

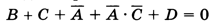
и закон поглащения

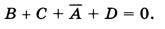
Для того, чтобы логическая сумма была равна нулю, каждое слагаемое должно быть равно нулю, поэтому А = 1, В = С = D = 0.

Способ 3. Можно построить таблицу истинности выражения в левой части и найти все варианты, при которых оно равно 0. Однако таблица истинности выражения с четырьмя переменными содержит 2⁴ = 16 строк, поэтому такой подход достаточно трудоёмок.

Пример 2. 

Требуется найти все решения уравнения

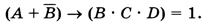
Преобразуем выражение, раскрыв импликацию через НЕ и ИЛИ и применив закон де Моргана:

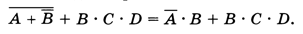
Вынося за скобку В, получаем

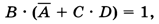
откуда сразу следует, что В = 1. Таким образом, количество решений исходного уравнения равно количеству решений уравнения ¬А + С • D = 1.

Если логическая сумма равна 1, то хотя бы одно слагаемое равно 1 (или оба одновременно). Во-первых, уравнение ¬А + С • D = 1 обращается в тождество при ¬А = 1, т. е. при А = 0. При этом получаем четыре решения, для всех возможных комбинаций С и D. Во-вторых, это равенство выполняется при С • D = 1, т. е. при С = D = 1 и любом А. Это даёт ещё два решения. Но из этих шести решения два совпадают: А = 0, С = 1, D = 1. Поэтому уравнение имеет всего пять разных решений.

3. КОЛИЧЕСТВО РЕШЕНИЙ УРАВНЕНИЯ.

Пример 1. 

Требуется найти число решений уравнения

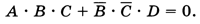
Здесь, в отличие от предыдущих задач, не нужно находить сами решения, нас интересует только их количество. Уравнение распадается на два:

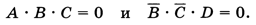
Каждое из них имеет достаточно много решений. Можно поступить следующим образом: сначала найти количество решений «обратного» уравнения, с единицей в правой части:

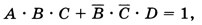
и затем вычесть его из 16 (общего количества различных комбинаций четырёх переменных). Уравнение А • В • С = 1 имеет два решения: А = В = С = 1 и любое D (0 или 1). Второе уравнение, ¬В • ¬С • D = 1, тоже имеет два решения: А — любое, В = С = 0, D = 1. Среди этих четырёх решений нет повторяющихся, поэтому исходное уравнение имеет 16 — 4 = 12 решений.

Пример 2. 

Требуется найти число решений уравнения

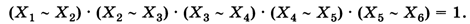
Так как каждая логическая переменная может принимать только значения 0 и 1, можно представить решение в виде 6-битной цепочки. Например, цепочка 010110 означает, что Х₁ = Х₃ = Х₆ = 0 и Х₂ = Х₄ = Х₅ = 1. Количество различных битовых цепочек длины 6 равно 2⁶ = 64, поэтому число решений уравнения — не более 64.

Для того чтобы логическое произведение было равно 1, необходимо, чтобы каждый сомножитель был равен 1. Это значит, что значения X_i и X_i+1 равны для всех i, т. е. соседние биты в цепочке должны быть равны. Это условие определяет всего две разрешённые цепочки, одна из которых состоит из одних нулей, вторая — из одних единиц. Поэтому уравнение имеет два решения: 000000 и 111111.

Пример 3. 

Требуется найти число решений уравнения

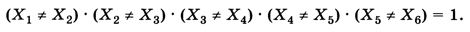
Так же как и в предыдущем примере, необходимо, чтобы каждый сомножитель был равен 1. Это значит, что значения X_i и X_i+1 не равны для всех i, т. е. соседние биты в цепочке должны быть разными. Это условие определяет всего две разрешённые цепочки, в которых биты чередуются: одна из них начинается с нуля, а вторая — с единицы. Поэтому уравнение имеет два решения: 010101 и 101010.

Пример 4. 

Требуется найти число решений уравнения

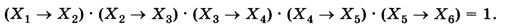
Импликация А —> В ложна только тогда, когда А = 1 и В = 0. Поэтому в битовой цепочке, которая является решением уравнения, не может встречаться последовательность 10, иначе какая-то импликация окажется ложной, и всё выражение в левой части будет равно 0. Поэтому существует всего 7 решений, все они имеют структуру «сначала нули, потом единицы»:

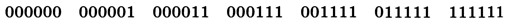
Обратите внимание, что количество решений логических уравнений, в отличие от количества решений «обычных уравнений», всегда конечно. Это связано с тем, что каждая переменная может принимать только два значения (0 и 1) и число разных комбинаций значений переменных конечно, оно равно 2ⁿ, где n — это количество переменных. Поэтому уравнение с n переменными имеет не более 2ⁿ решений.