Двоичные числа, как и десятичные, можно складывать в столбик, начиная с младшего разряда. При этом используют следующие правила (таблицу сложения):
0 + 0 = 0, 1 + 0=1, 1 + 1 = 102, 1 + 1 + 1 = 112.
В двух последних случаях, когда сумма 2 = 102 или 3 = 112 не может быть записана с помощью одного разряда, происходит перенос в следующий разряд.
Например, сложим в столбик 101102 и 1110112 Единицы сверху обозначают перенос из предыдущего разряда:

Вычитание выполняется почти так же, как и в десятичной системе. Вот основные правила:
0-0 = 0, 1-0=1, 1-1 = 0, 102 — 1 = 1.
В последнем случае приходится брать заём из предыдущего разряда. Именно этот вариант представляет наибольшие сложности, поэтому мы рассмотрим его подробно.
Чтобы понять принцип, временно вернёмся к десятичной системе. Вычтем в столбик из числа 21 число 9:
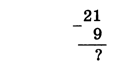
Поскольку из 1 нельзя вычесть 9, нужно взять заём из предыдущего разряда, в котором стоит 2. В результате к младшему разряду добавляется 10 (основание системы счисления), а в предыдущем цифра 2 уменьшается до 1. Теперь можно выполнить вычитание: 1 + 10-9 = 2. В старшем разряде вычитаем из оставшейся единицы ноль:
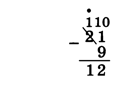
Здесь точкой сверху обозначен разряд, из которого берётся заём.
Более сложный случай — заём из дальнего (не ближайшего) разряда. Вычтем 9 из 2001. В этом случае занять из ближайшего разряда не удаётся (там 0), поэтому берём заём из того разряда, где стоит цифра 2. Все промежуточные разряды в результате заполняются цифрой 9, это старшая цифра десятичной системы счисления:
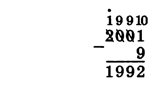
Что изменится в двоичной системе? Когда берётся заём, в «рабочий» разряд добавляется уже не 10, а 102 = 2 (основание системы счисления), а все «промежуточные» разряды (между «рабочим» и тем, откуда берется заём) заполняются не девятками, а единицами (старшей цифрой системы счисления). Например:
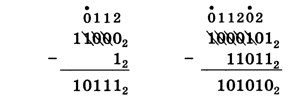
Если требуется вычесть большее число из меньшего, вычитают меньшее из большего и ставят у результата знак «минус»:
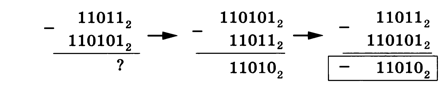
Умножение и деление столбиком в двоичной системе выполняются практически так же, как и в десятичной системе (но с использованием правил двоичного сложения и вычитания):

При вычислениях в восьмеричной системе нужно помнить, что максимальная цифра — это 7. Перенос при сложении возникает тогда, когда сумма в очередном разряде получается больше 7.
Заём из старшего разряда равен 108 = 8, а все «промежуточные» разряды заполняются цифрой 7 — старшей цифрой системы счисления. Приведём примеры сложения и вычитания:
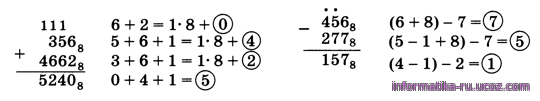
В примере на сложение запись 1*8 + 2 означает, что получилась сумма, большая 7, которая не помещается в один разряд.
Единица идёт в перенос, а двойка остаётся в этом разряде. При выполнении вычитания запись «-1» означает, что из этого разряда раньше был заём (его значение уменьшилось на 1), а запись «+8» — заём из старшего разряда.
При выполнении сложения нужно помнить, что в системе с основанием 16 перенос появляется тогда, когда сумма в очередном разряде превышает 15. Удобно сначала переписать исходные числа, заменив все буквы на их численные значения:

При вычитании заём из старшего разряда равен 1016 = 16, а все «промежуточные» разряды заполняются цифрой F — старшей цифрой системы счисления.
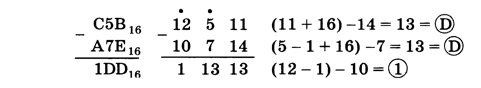
Если нужно работать с числами, записанными в разных системах счисления, их сначала приводят к какой-нибудь одной системе. Например, пусть требуется сложить 538 и 5616 и записать результат в двоичной системе счисления. Здесь можно выполнять сложение в двоичной, восьмеричной, десятичной или шестнадцатеричной системах. Переход к десятичной системе, а потом перевод результата в двоичную трудоёмок. Практика показывает, что больше всего ошибок делается при вычислениях именно в двоичной системе, поэтому лучше выбирать восьмеричную или шестнадцатеричную систему. Переведём число 538 в шестнадцатеричную систему через двоичную:
538 = 101 0112 = 10 10112 = 2В16.
Теперь выполним сложение:
2В16 + 5616 = 8116
и переведём результат в двоичную систему:
8116 = 1000 00012.









