Ключевые слова:

следование
ветвление
повторение

линейные алгоритмы

разветвляющиеся алгоритмы

циклические алгоритмы

§2.4 Основные алгоритмические конструкции

 

 

Человеку в жизни приходится решать множество различных за­дач. Решение каждой из них описывается своим алгоритмом, и раз­нообразие этих алгоритмов очень велико. Вместе с тем для записи любого алгоритма достаточно трёх основных алгоритмических кон­струкции (структур): следования, ветвления, повторения. Это поло­жение выдвинул и доказал Э. Дейкстра в 70-х гг. прошлого века.

Эдсгер Вибе Дейкстра (1930-2002) — выдающийся нидерландский учёный, идеи которого оказали огромное влияние на развитие компьютерной индустрии.

2.4.1. Следование

Следование — алгоритмическая конструкция, отображающая естест­венный, последовательный порядок действий. Алгоритмы, в которых используется только структура «следование», называются j алгоритмами.

Графическое представление алгоритмической конструкции «сле­дование» приведено на рис. 2.8.

 

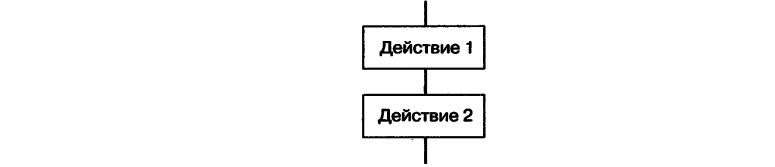
Рис. 2.8. Алгоритмическая конструкция «следование»

 

Пример 1. Линейный алгоритм приготовления отвара шиповника.

 

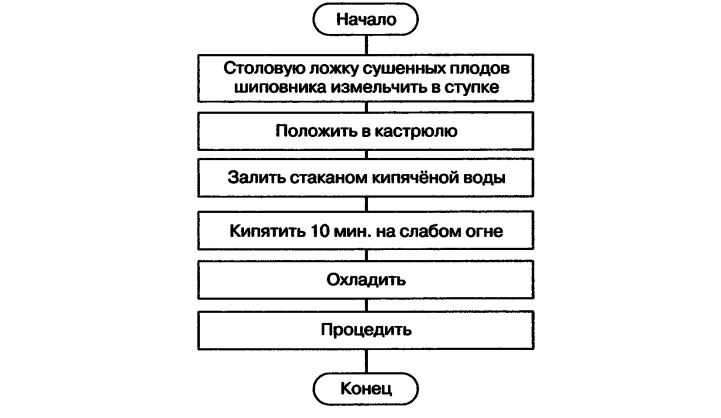
Обратите внимание, что многие из предписаний этого алгоритма могут потребовать детализации — представления в виде некоторой совокупности более мелких предписаний.

 

Пример 2. У исполнителя Робот есть четыре команды перемеще­ния (вверх, вниз, влево и вправо), при выполнении каждой из них Робот перемещается на одну клетку в соответствующем направле­нии. По команде закрасить Робот закрашивает клетку, в которой он находится. Запишем линейный алгоритм, исполняя который

Робот нарисует на клетчатом поле следующий узор и вернётся в ис­ходное положение, обозначенное звёздочкой:

 

Пример 3. Дан фрагмент линейного алгоритма:

 

х:=2

у:=х*х

у:=у*у

х:=у*х
s:=x+y

Выясним, какое значение получит переменная s после выполне­ния этого фрагмента алгоритма. Для этого составим таблицу значе­ний переменных, задействованных в алгоритме:

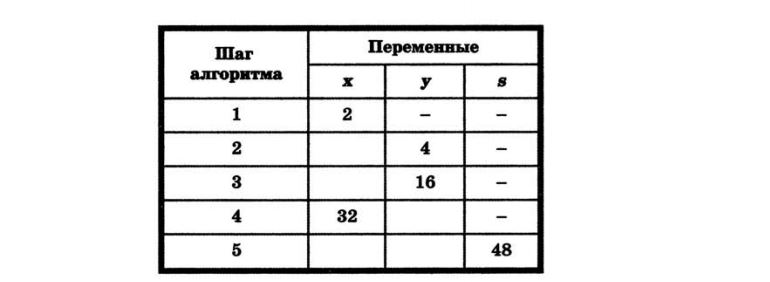
Составленная нами таблица значений переменных моделирует ра­боту исполнителя этого алгоритма.

Пример 4. Некоторый исполнитель может выполнять над целыми числами кроме операций сложения, вычитания, умножения и деле­ния ещё две операции: с помощью операции div вычисляется целое частное, с помощью операции mod — остаток.

Например: 5 div 2 = 2; 5 mod 2 = 1; 2 div 5 = 0; 2 mod 5 = 2.

Покажем, как с помощью этих операций можно реализовать ал­горитм работы кассира, выдающего покупателю сдачу (s) наимень­шим количеством банкнот по 500 (k500), 100 (k100), 50 (k50) и 10 (k10) рублей.

k500:=s   div   500

s:=s  mod   500

k100:=s   div   100

s:=s  mod   100

k50:=s   div   50

s:=s   mod   50

k10:=s   div   10

Исполните алгоритм для s = 745 и s = 1864. Составьте соответствующие таблицы значений переменных.

Ознакомьтесь с имеющимся в Единой коллекции цифровых образова­тельных ресурсов модулем для коллективной работы «Линейные алгорит­мы» (217039). Совместно с друзьями постарайтесь составить алгоритмы для имеющихся в модуле задач. Пройдите тестирование.