По образцу
Ключевые слова:
§2.3 Объекты алгоритмов
Ключевые слова:
- величина
- константа
- переменная
- тип
- имя
- присваивание
- выражение
- таблица
2.3.1. Величины
Алгоритмы описывают последовательность действий, производимых над некоторыми объектами, определёнными условием задачи. Например, при решении задачи о начислении зарплаты сотрудникам предприятия такими объектами могут быть табельный номер сотрудника, его фамилия, имя, отчество, оклад, отработанное время и т. д.
В информатике отдельный информационный объект (число, символ, строка, таблица и др.) называется величиной.
Величины делятся на постоянные (константы) и переменные. Постоянной (константой) называется величина, значение которой указывается в тексте алгоритма и не меняется в процессе его исполнения. Переменной называется величина, значение которой меняется в процессе исполнения алгоритма. При исполнении алгоритма в каждый момент времени переменная обычно имеет значение, называемое текущим значением.
Пример 1.
Величины, выражающие количество дней в неделе, ускорение свободного падения, количество дней в первой декаде месяца, являются константами. Величины, выражающие количество дней в месяце, пульс человека, количество дней в третьей декаде месяца, являются переменными.
В алгоритмах над величинами выполняются некоторые операции. Например:
- арифметические операции +, -, * (умножение), / (деление);
- операции отношения <, >, <=, >=, =, ;
- логические операции И, ИЛИ, НЕ.
Объекты, над которыми выполняются операции, называются операндами. Не всякий объект может быть операндом для выполнения любой операции. Например, текст не может быть объектом для выполнения арифметических операций; отрицательное число не может быть операндом для извлечения квадратного корня и т. д.
Множество величин, объединённых определённой совокупностью допустимых операций, называют величинами определённого типа. При составлении алгоритмов используют величины числового (целого и вещественного), символьного, литерного и логического типов.
В математике и физике оперируют числовыми величинами — натуральными, целыми, действительными числами. При составлении алгоритмов чаще всего используют числовые величины целого и вещественного типов, которые в алгоритмическом языке обозначаются цел и вещ соответственно.
В задачах, возникающих в повседневной жизни, встречаются и нечисловые величины, значениями которых являются символы, слова, тексты и др. При составлении алгоритмов обработки текстовой информации используют величины символьного (сим) и литерного (лит) типов. Значением символьной величины является один символ: русская или латинская буква, цифра, знак препинания или другой символ. Значением литерной величины является последовательность символов. Иногда эту последовательность называют строкой или цепочкой. Литерные значения в алгоритме записывают в кавычках, например: 'алгоритм', 'литерная величина', '2011’.
Величины логического (лог) типа могут принимать всего два значения:
- ДА (ИСТИНА, TRUE, 1);
- НЕТ (ЛОЖЬ, FALSE, 0).
Для ссылок на величины используют их имена (идентификаторы). Имя величины может состоять из одной или нескольких латинских букв, из латинских букв и цифр: А1, М, АР. Рекомендуется выбирать мнемонические имена, т. е. имена, отражающие суть объектов решаемой задачи, например, SUMMA, PLAN, CENA и т. д.
Если величину представить как ящик, содержимым которого является некоторое значение, то имя величины — это ярлык, повешенный на ящик.
2.3.2. Выражения
Выражение — языковая конструкция для вычисления значения с помощью одного или нескольких операндов.
Выражения состоят из операндов (констант, переменных, функций), объединённых знаками операций. Выражения записываются в виде линейных последовательностей символов (без подстрочных и надстрочных символов, обыкновенных дробей и т. д.); знаки операций пропускать нельзя. Порядок выполнения операций определяется скобками и приоритетом (старшинством) операций; операции одинакового приоритета выполняются слева направо.
Различают арифметические, логические и строковые выражения.
Арифметические выражения служат для определения числового значения. Например, 2*х+3 — арифметическое выражение, значение которого при х = 1 равно пяти, а при х = -1 — единице. Выражение sqrt(x) служит для обозначения операции извлечения квадратного корня из х (sqrt(x)).
Логические выражения описывают некоторые условия, которые могут удовлетворяться или не удовлетворяться. Логическое выражение может принимать одно из двух значений — ИСТИНА или ЛОЖЬ. Например, логическое выражение х>5) и (х<10) определяет принадлежность точки х интервалу (5; 10):

При х = 6 значение этого выражения — ИСТИНА, а при х = 12 — ЛОЖЬ.
Строковые выражения состоят из величин (констант, переменных) символьного и литерного типов, соответствующих функций и операций сцепления (присоединения). Операция сцепления обозначается знаком «+> и позволяет соединить в одну последовательность несколько последовательностей символов. Значениями строковых выражений являются последовательности символов. Например, если А = ‘том’, то значение строкового выражения 'a’+А есть 'атом'.
2.3.3. Команда присваивания
Задать конкретное значение величины можно с помощью операции присваивания, которая записывается так:
<имя переменной> := <выражение>
Знак «:=» читается: «присвоить». Например, запись А := В + 5 читается так: «переменной А присвоить значение выражения В плюс 5».
Знаки присваивания «:=» и равенства «=» — разные знаки:
- знак «=» означает равенство двух величин, записанных по обе стороны от этого знака;
- знак «:=» предписывает выполнение операции присваивания.
Например, запись А: = А + 1 выражает не равенство значений А и А + 1, а указание увеличить значение переменной А на единицу.
При выполнении команды присваивания сначала вычисляется значение выражения, стоящего справа от знака «:=», затем результат присваивается переменной, стоящей слева от знака «:=». При этом тип выражения должен быть совместим с типом соответствующей переменной.
Свойства присваивания:
- пока переменной не присвоено значение, она остаётся неопределённой;
- значение, присвоенное переменной, сохраняется в ней вплоть до выполнения следующего присваивания этой переменной нового значения;
- если мы присваиваем некоторой переменной очередное значение, то предыдущее её значение теряется безвозвратно.
Пример 2. Составим алгоритм, в результате которого переменные А и В литерного типа обменяются своими значениями.
Решение вида
А:=В
В:=А
неверно, так как после выполнения первой команды присваивания первоначальное значение переменной А будет безвозвратно утеряно. Вторая команда присвоит переменной В текущее значение переменной А. В результате обе переменные получат одно и то же значение.
Для поиска правильного решения воспользуемся аналогией. Если требуется перелить жидкость из сосуда 1 в сосуд 2, а из сосуда 2 — в сосуд 1, то без дополнительного сосуда 3 здесь не обойтись. Алгоритм переливаний представлен на рис. 2.4.
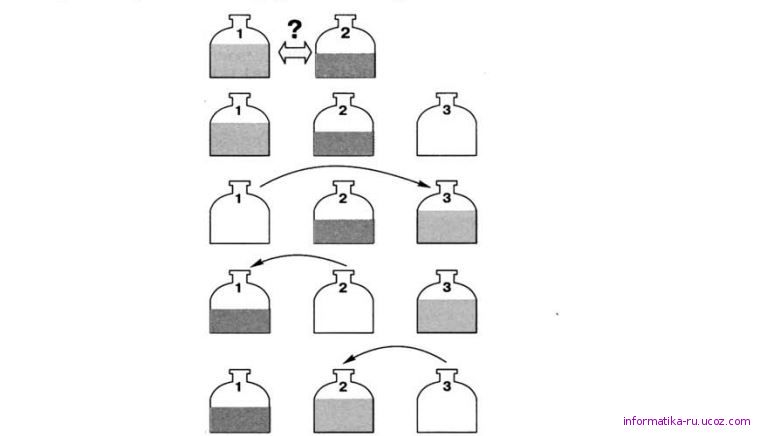
Рис. 2.4. Алгоритм переливаний жидкостей
Для решения исходной задачи введём промежуточную переменную М. Алгоритм обмена значениями переменных А и В запишем так:
алг обмен значениями {лит А, В)
арг А, В
рез А, В
нач лит М
М:=А
А:=В
В:=М
кон
Если А и В — числовые величины, то обмен их значениями мож-о организовать и без промежуточной переменной, например так:
А:=А+В
В:=А-В
А:=А-В
2.3.4.Табличные величины
В практической деятельности человек часто использует всевозможные таблицы. Это, например, список учащихся в классном журнале, табель успеваемости, таблица результатов спортивных соревнований и т. д. Чаще всего встречаются линейные и прямоугольные таблицы.
Линейная таблица (одномерный массив) представляет собой набор однотипных данных, записанных в одну строку или один столбец. Элементы строки (столбца) всегда нумеруются. Например, с помощью линейной таблицы могут быть представлены дни недели (рис. 2.5, а) или количество уроков, пропущенных учеником в течение 5-дневной учебной недели (рис. 2.5, б).
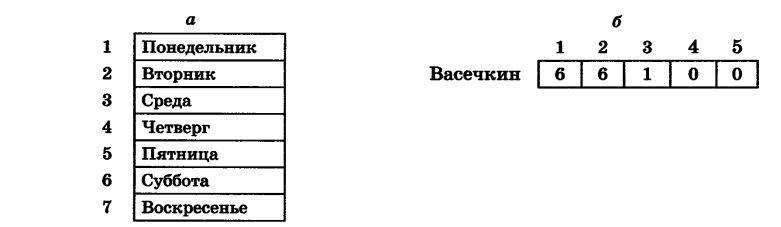
Рис. 2.5. Примеры линейных таблиц
Прямоугольная таблица (двумерный массив) — это упорядоченный некоторым образом набор строк (столбцов), содержащих одинаковое количество элементов. Строки прямоугольных таблиц имеют свою нумерацию, столбцы — свою. Например, с помощью прямоугольной таблицы можно представить количество уроков, пропущенных всеми учениками 8 класса в течение 5-дневной учебной недели (рис. 2.6)
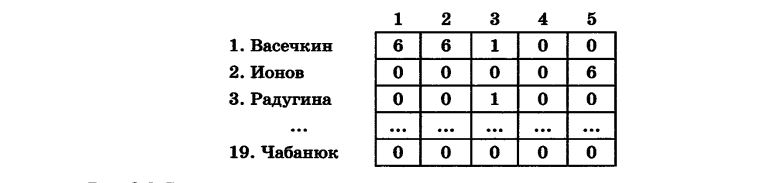
Рис. 2.6. Пример прямоугольной таблицы
Всей совокупности элементов табличной величины даётся одно имя. Элементы различают по их номерам, называемым индексами. Индекс записывается в квадратных скобках сразу за именем таблицы.
Если первую из рассмотренных нами таблиц (см. рис. 2.5, а) назвать WEEK, то WEEK[1] = 'понедельник', WEEK[6] - 'суббота*. Назовём третью из рассмотренных таблиц LES. Тогда LES[1,1] = 6, L-ES[2,5] = 6, LES[S,4] = 0.
Образно линейная и прямоугольная таблицы показаны на рис. 2.7.
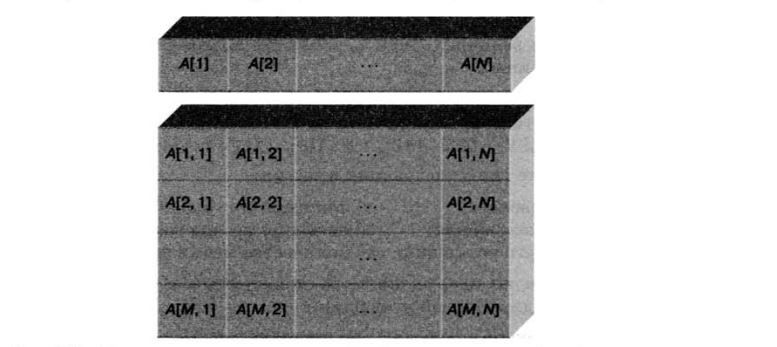
Рис. 2.7. Образное представление линейной и прямоугольной таблиц
САМОЕ ГЛАВНОЕ
В информатике отдельный информационный объект (число, символ, строка, таблица и др.) называется величиной.
Величины делятся на постоянные (их значения указываются в тексте алгоритма и не меняются в процессе его исполнения) и переменные (их значения меняются в процессе исполнения алгоритма). При составлении алгоритмов используют величины целого, вещественного, логического, символьного и литерного типов.
Для ссылок на величины используют их имена (идентификаторы). Имя величины может состоять из одной или нескольких латинских букв, из латинских букв и цифр. Таблица (массив) — набор некоторого числа однотипных элементов, которым присвоено одно имя. Положение элемента в таблице однозначно определяется его индексами.
Вопросы и задания
- Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.
- Что такое величина? Чем отличаются постоянные и переменные величины?
- Величины каких типов используются при записи алгоритмов?
- Укажите тип величины, если её значение равно: 2010; 14.48;
ДА"; FALSE, -125; 142'; 1,4 • 105; Л23Е-2; 'пять'.
5. Определите типы следующих величин:
а) вес человека; г) площадь фигуры;
б) марка автомобиля; д) название месяца года;
в) год вашего рождения; е) количество мест в самолёте.
6. Приведите по одному примеру допустимых и недопустимых
значений для каждой из величин:
а) температура человека; в) площадь страны;
б) скорость автомашины; г) название дня недели.
- Для чего предназначена команда присваивания? Каковы её
основные свойства? - Какие команды присваивания составлены правильно?
а)А:=В б)А=В
в) А=В+1
г)А+1:=А
9. Придумайте свой алгоритм обмена значениями числовых пере-
менных Аи В.
- Сколько промежуточных переменных потребуется для того, чтобы переменной А было присвоено значение переменной В, переменной В — значение переменной С, а переменной С — значение переменной А? Запишите соответствующий алгоритм на алгоритмическом языке
- После выполнения команды присваивания х:=х+у значение
переменной х равно 3, а значение переменной у равно 5. Чему были равны значения переменных х и у до выполнения указанной команды присваивания?
- Что называют выражением? Каковы основные правила записи выражений?
- Переведите из линейной записи в общепринятую:
а) а * Ь I с; г) (а + 6) / с;
б) а I Ь * с; Д) а + 6 / с + d;
в) а + Ъ I с; е) (а + Ь) / (с + d).
14. Запишите на алгоритмическом языке:
а) ах2 + Ьх + с;
„ at2 6)v + —;
,х»
15. Запишите логическое выражение, истинное при выполненииуказанного условия и ложное в противном случае:
а) х принадлежит отрезку [О, 1];
б) х лежит вне отрезка [О, 1];
в) каждое из чисел х, у положительно;
г) хотя бы одно из чисел х, у положительно;
д) ни одно из чисел х, у не является положительным;
е) только одно из чисел х, у положительно.
16. Изобразите в декартовой прямоугольной системе координат область, в которой и только в которой истинно следующее логическое выражение:
а) (х>=-1) и (х<=1) и (у>=-1) и (у<=1);
б) (у>=х) и (у>=-х) и (у<=1).
17. Запишите логическое выражение, принимающее значение TRUE, когда точка с координатами (х, у) принадлежит закрашенной области.
18. Запишите команду присваивания, в результате выполнения которой логическая переменная t получает значение TRUE, если выполняется указанное условие, и значение FAI£E в противном случае:
а) х — положительное число;
б) хотя бы одно из чисел х, у, г равно нулю;
в) числа х, у, г равны между собой.
19. Какие вз приведённых ниже величин целесообразно представлять с помощью таблиц?
Величины: список учеников класса, рост учеников класса, средний рост учеников класса, оценка ученика по физике, средний балл ученика по физике, оценки учеников за контрольную работу по информатике, длины сторон треугольника, длины сторон нескольких треугольников, названия дней недели, имя человека, площадь фигуры, периметры нескольких прямоугольников, самая холодная температура воздуха в январе, количество девочек в классе, самая дождливая декада июня.








